
 的
的
| A.2 | B.4 | C. | D. |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:解答题
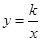 的图象在第一象限内的任意两点A、B作x轴的垂线,垂足分别为C、D,连接AO、BO和AB,AC和OB的交点为E,设△AOB与梯形ACDB的面积分别为S
的图象在第一象限内的任意两点A、B作x轴的垂线,垂足分别为C、D,连接AO、BO和AB,AC和OB的交点为E,设△AOB与梯形ACDB的面积分别为S 与S
与S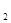 ,
,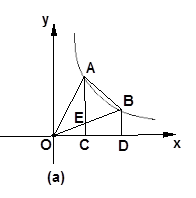

 与S
与S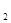 的大小;
的大小;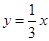 与双曲线
与双曲线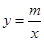 交于M、N点,且点M的纵坐标为2.
交于M、N点,且点M的纵坐标为2.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
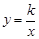 经过点A.若S△BEC=8.则k的值为______.
经过点A.若S△BEC=8.则k的值为______.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
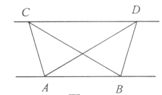
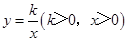 的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.证明:MN∥EF.
的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.证明:MN∥EF.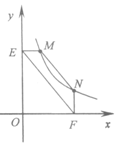
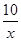 的图象上,且M(2,m),N是第三象限内反比例函数y=
的图象上,且M(2,m),N是第三象限内反比例函数y=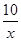 的图象上一动点.过点M作ME⊥y轴,过点N作EF⊥x轴,垂足分别为E,F.说明MN∥EF.并求当四边形MEFN的面积为12时点N的坐标.
的图象上一动点.过点M作ME⊥y轴,过点N作EF⊥x轴,垂足分别为E,F.说明MN∥EF.并求当四边形MEFN的面积为12时点N的坐标.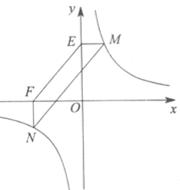
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).
上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).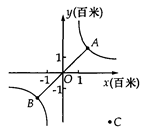
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com