
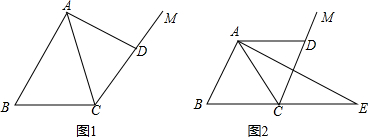
分析 (1)①先根据三角形的内角和求∠ACB=70°,由平行线的性质得:∠DAC=70°,利用角平分线得:∠DAE=35°,最后利用平行线的内错角相等得结论;
②设∠CAE=x,∠BAC=y,在△ACD和△ABE中根据三角形内角和表示∠ADC和∠AEC,可得结论;
(2)如图3,设∠ABC=x,∠EAD=y,则∠ACB=nx,∠CAE=ny,在△ACE中根据外角的性质得:∠AEC=nx-ny=n(x-y),在△ADC中,根据三角形内角和可得∠ADC的度数,由此可得结论.
解答 解:(1)①如图2,∵∠BAC=40°,
∴∠ACB+∠ABC=180°-40°=140°,
∵∠ACB=∠ABC,
∴∠ACB=70°,
∵AD∥BC,
∴∠DAC=∠ACB=70°,
∵AE平分∠DAC,
∴∠DAE=$\frac{1}{2}$∠DAC=$\frac{1}{2}$×70°=35°,
∵AD∥BC,
∴∠AEC=∠DAE=35°,
故答案为:35°;
②∠ADC=2∠AEC,
理由是:设∠CAE=x,∠BAC=y,则∠EAD=x,∠ABC=$\frac{180-y}{2}$,
∵AB∥CM,
∴∠ACM=∠BAC=y,
∴∠ADC=180-2x-y,
△ABE中,∠AEC=180-x-y-$\frac{180-y}{2}$=90-x-$\frac{y}{2}$,
∴∠ADC=2∠AEC;
(2)∠AEC=$\frac{n}{n+1}$∠ADC,理由是: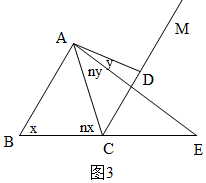
如图3,设∠ABC=x,∠EAD=y,则∠ACB=nx,∠CAE=ny,
△ACE中,∠AEC=nx-ny=n(x-y),
∴x-y=$\frac{1}{n}∠AEC$,
△ABC中,∠BAC=180-nx-x,
∵AB∥CM,
∴∠ACD=∠BAC=180-nx-x,
△ADC中,∠ADC=180-ny-y-(180-nx-x)=-ny-y+nx+x=n(x-y)+(x-y)=(x-y)(n+1),
∴x-y=$\frac{1}{n+1}$∠ADC,
∴$\frac{1}{n}$∠AEC=$\frac{1}{n+1}$∠ADC,
∴∠AEC=$\frac{n}{n+1}$∠ADC.
故答案为:∠AEC=$\frac{n}{n+1}$∠ADC.
点评 本题考查了平行线的性质、角平分线的定义、三角形内角和定理、外角的性质,设未知数,根据三角形内角和为180°或外角性质列式可解决问题.


科目:初中数学 来源: 题型:填空题
 如图,在边长为1的正方形ABCD中,点A的坐标为(1,1),AD∥x轴,动点P沿B→A→D→C→B运动,以点P为顶点的抛物线y=ax2+bx+c(a≠0)交x轴于M、N两点(点M在点N的左边),当点P运动时,该抛物线随之平移.若点M的横坐标的最小值为-1,则点N的横坐标的最大值为4.
如图,在边长为1的正方形ABCD中,点A的坐标为(1,1),AD∥x轴,动点P沿B→A→D→C→B运动,以点P为顶点的抛物线y=ax2+bx+c(a≠0)交x轴于M、N两点(点M在点N的左边),当点P运动时,该抛物线随之平移.若点M的横坐标的最小值为-1,则点N的横坐标的最大值为4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
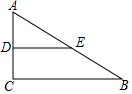 如图所示,在△ABC中,∠ACB=90°,AC=5,AB=13,点D是AC的中点,过点D作DE∥BC,交AB于E点,则DE的长为( )
如图所示,在△ABC中,∠ACB=90°,AC=5,AB=13,点D是AC的中点,过点D作DE∥BC,交AB于E点,则DE的长为( )| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com