
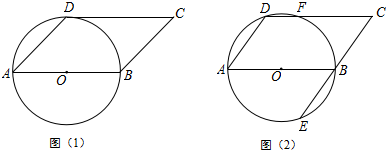
分析 (1)如图1中,连接OD,欲证明CD是切线,只要证明OD⊥DC即可.
(2)如图2中,连接DE,EF,BD,首先证明DE是直径,再根据EF2=DE2-DF2=CE2-CF2,设DF=x,则CF=10-x,列出方程即可解决.
解答 (Ⅰ)证明:连接OD.
∵∠A=45°,OA=OD,
∴∠A=∠ADO=45°,
∴∠BOD=90°.
∵四边形ABCD 是平行四边形,
∴AB∥CD.
∴∠CDO+∠BOD=180°.
∴∠CDO=∠BOD=90°.
∴OD⊥DC,
∴CD与⊙O相切.
(Ⅱ)如图2中,连接DE,EF,BD.
∵AB是⊙O直径,
∴∠ADB=90°.
∵AD∥BC,
∴∠ADB=∠EBD=90°.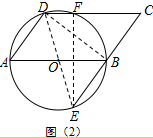
∴DE是⊙O直径.
∴DE=AB=CD=10.
∴BE=BC=AD=6.
在Rt△DEF和Rt△CEF中,EF2=DE2-DF2,EF2=CE2-CF2
∴DE2-DF2=CE2-CF2.
设 DF=x,则CF=10-x.
∴102-x2=122-(10-x)2.
解得$x=\frac{14}{5}$.即$DF=\frac{14}{5}$.
点评 本题考查切线的性质、平行四边形的性质、圆的有关性质、勾股定理等知识,学会转化的思想,把问题转化为方程解决,添加辅助线是解题的关键,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O是△ABC的外接圆,AC是直径,点E是AB的中点,延长EO交⊙O于D点,若BC=DC,AB=2$\sqrt{3}$,求$\widehat{AD}$的长度.
如图,⊙O是△ABC的外接圆,AC是直径,点E是AB的中点,延长EO交⊙O于D点,若BC=DC,AB=2$\sqrt{3}$,求$\widehat{AD}$的长度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
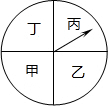 如图,将一个可以自由旋转的转盘等分成甲、乙、丙、丁四个扇形区域,若指针固定不变,转动这个转盘一次(如果指针指在等分线上,那么重新转动,直至指针指在某个扇形区域内为止),则指针指在丙区域内的概率是( )
如图,将一个可以自由旋转的转盘等分成甲、乙、丙、丁四个扇形区域,若指针固定不变,转动这个转盘一次(如果指针指在等分线上,那么重新转动,直至指针指在某个扇形区域内为止),则指针指在丙区域内的概率是( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 至少有1个球是黑球 | B. | 至少有1个球是白球 | ||
| C. | 至少有2个球是黑球 | D. | 至少有2个球是白球 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{20}$ | B. | $\sqrt{4}$ | C. | $\sqrt{8}$ | D. | $\sqrt{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com