
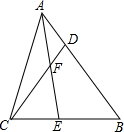
 已知,如图,在△ABC中,AE是角平分线,D是AB上的点,AE、CD相交于点F.
已知,如图,在△ABC中,AE是角平分线,D是AB上的点,AE、CD相交于点F.分析 (1)先根据∠ACB=∠CDB=90°得出∠B=90°-∠DCB,∠ACD=90°-∠DCB,再由AE平分∠CAB即可得出结论;
(2)①根据三角形外角的性质可得出∠CFE=∠ACD+$\frac{1}{2}$∠CAB,∠CEF=∠B+$\frac{1}{2}$∠CAB,故∠CFE-∠CEF=∠B-∠ACD,再由∠B=180°-m-∠DCB,∠ACD=m-∠DCB即可得出结论;
②根据∠CEF小于∠CFE可知∠CEF-∠CFE<0,故180°-2m<0,进而可得出结论.
解答 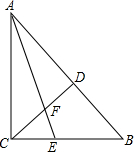 解:(1)∵∠ACB=∠CDB=90°,
解:(1)∵∠ACB=∠CDB=90°,
∴∠B=90°-∠DCB,∠ACD=90°-∠DCB,
∴∠B=∠ACD.
∵AE平分∠CAB,
∴∠CFE=∠ACD+$\frac{1}{2}$∠CAB,∠CEF=∠B+$\frac{1}{2}$∠CAB,
∴∠CFE=∠CEF;
(2)①∵∠CFE=∠ACD+$\frac{1}{2}$∠CAB,∠CEF=∠B+$\frac{1}{2}$∠CAB,
∴∠CFE-∠CEF=∠B-∠ACD.
∵∠B=180°-m-∠DCB,∠ACD=m-∠DCB,
∴∠CEF-∠CFE=(180°-m-∠DCB)-(m-∠DCB)=180°-2m;
②存在.
∵要使∠CEF小于∠CFE,则∠CEF-∠CFE<0,
∴180°-2m<0,解得m>90°,
∴当90°<m<180°时,∠CEF的值小于∠CFE.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.


科目:初中数学 来源: 题型:解答题
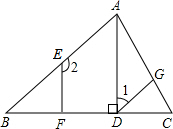 如图,已知AD是△ABC的高,点E、G分别在AB、AC上,EF⊥BC,垂足为F,∠CGD=∠BAC,若∠1=50°,求∠2和∠B的度数.
如图,已知AD是△ABC的高,点E、G分别在AB、AC上,EF⊥BC,垂足为F,∠CGD=∠BAC,若∠1=50°,求∠2和∠B的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购物总金额(原价) | 优惠率 |
| 不超过5000元的部分 | 10% |
| 超过5000元且不超过10000元的部分 | 20% |
| 超过10000元且不超过20000元的部分 | 30% |
| … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com