
 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD,下列结论:①∠BAE=30°;②△ABE∽△AEF;③△ABE∽△ECF;④△ADF∽△ECF.其中正确的是( )
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD,下列结论:①∠BAE=30°;②△ABE∽△AEF;③△ABE∽△ECF;④△ADF∽△ECF.其中正确的是( )| A. | ①②③ | B. | ②③ | C. | ③④ | D. | ②③④ |
分析 根据已知条件得到BE=$\frac{1}{2}$AB,由三角函数的定义得到tan∠BAE=$\frac{BE}{AB}$=$\frac{1}{2}$,于是得到∠BAE≠30°;故①错误;根据已知条件得到$\frac{AB}{CE}$=$\frac{BE}{CF}$=2,且∠B=∠C,得到△ABE∽△ECF,③正确;根据余角的性质得到∠AEF=90°,根据相似三角形的性质得到$\frac{AE}{EF}$=$\frac{AB}{EC}$=2,推出△ABE∽△AEF,②正确;由于$\frac{DA}{CE}$=2,$\frac{DF}{CF}$=3,得到$\frac{AD}{CE}$≠$\frac{DF}{CF}$,于是得到△ADF和△ECF不相似,④错误.
解答 解:在正方形ABCD中,
∵AB=BC,
∵E是BC的中点,
∴BE=$\frac{1}{2}$AB,
∴tan∠BAE=$\frac{BE}{AB}$=$\frac{1}{2}$,
∴∠BAE≠30°;故①错误;
∵E为BC中点,CF:CD=1:4,
∴$\frac{AB}{CE}$=$\frac{BE}{CF}$=2,且∠B=∠C,
∴△ABE∽△ECF,
∴③正确;
∴∠BAE=∠FEC,且∠BAF+∠AFB=90°,
∴∠AFB+∠FEC=90°,
∴∠AEF=90°,
∵△ABE∽△ECF,
∴$\frac{AE}{EF}$=$\frac{AB}{EC}$=2,
∴$\frac{AB}{AE}$=$\frac{CE}{EF}$=$\frac{BE}{EF}$,且∠ABE=∠AEF=90°,
∴△ABE∽△AEF,
∴②正确;
∵$\frac{DA}{CE}$=2,$\frac{DF}{CF}$=3,
∴$\frac{AD}{CE}$≠$\frac{DF}{CF}$,
∴△ADF和△ECF不相似,
∴④错误,
综上可知正确的为:②③,
故选B.
点评 本题主要考查相似三角形的判定和性质,掌握相似三角形的判定方法是解题的关键,注意正方形性质的运用.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
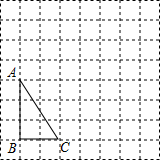 如图,在方格纸上,以格点连线为边的三角形叫做格点三角形,请按要求完成下列操作:先将格点△ABC绕A点逆时针旋转90°得到△A1B1C1,再将△A1B1C1沿直线B1C1作轴对称得到△A2B2C2.
如图,在方格纸上,以格点连线为边的三角形叫做格点三角形,请按要求完成下列操作:先将格点△ABC绕A点逆时针旋转90°得到△A1B1C1,再将△A1B1C1沿直线B1C1作轴对称得到△A2B2C2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在下列网格中建立平面直角坐标系如图,每个小正方形的边长均为1个单位长度.已知A(1,1)、B(3,4)和C(4,2).
在下列网格中建立平面直角坐标系如图,每个小正方形的边长均为1个单位长度.已知A(1,1)、B(3,4)和C(4,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com