
 如图,已知四边形ABCD内接于半径为4的⊙O中,且∠C=2∠A,则BD=4$\sqrt{3}$.
如图,已知四边形ABCD内接于半径为4的⊙O中,且∠C=2∠A,则BD=4$\sqrt{3}$. 分析 连接OD、OB,过点O作OF⊥BD,垂足为F,由垂径定理可知DF=BF,∠DOF=∠BOF,再由圆内接四边形的性质求出∠A的度数,故可得出∠BOD的度数,再由锐角三角函数的定义求出BF的长,进而可得出结论.
解答 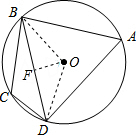 解:连接OD、OB,过点O作OF⊥BD,垂足为F,
解:连接OD、OB,过点O作OF⊥BD,垂足为F,
∵OF⊥BD,
∴DF=BF,∠DOF=∠BOF.
∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°.
∵∠C=2∠A,
∴∠A=60°,
∴∠BOD=120°,
∴∠BOF=60°.
∵OB=4,
∴BF=OB•sin∠BOF=4×sin60°=2$\sqrt{3}$,
∴BD=2BF=4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解答此题的关键.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:填空题
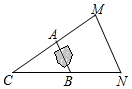 如图,A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200m,则A,B间的距离为100m.
如图,A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200m,则A,B间的距离为100m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 64(x+1)2=50 | B. | 50(x+1)2=64 | C. | 64(1-x)2=50 | D. | 50(1-x)2=64 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y3<y1<y2 | B. | y1<y2<y3 | C. | y2<y1<y3 | D. | y3<y2<y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年份 | 2014 | 2015 | 2016 | 2017(预计) |
| 快递件总量(亿件) | 140 | 207 | 310 | 450 |
| 电商包裹件(亿件) | 98 | 153 | 235 | 351 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com