

���� ��1������30���ֱ����������CD��ED�������������ʽ���AEC�������
��2���������ߣ�����ȫ�������Σ�֤����AFM�ա�ADH����AM=AH��FM=DH�����MAH�ǵ���ֱ�������Σ���MH=$\sqrt{2}$AH�������߶εĺʹ���ý��ۣ�
��3��ȡAC���е�O������ON��OD���ڡ�DON�У��������������߹�ϵ���ɳ�DN��ȡֵ��Χ��
��� �⣺��1����ͼ1����Rt��EDC�У��ߡ�EDC=30�㣬
��ED=$\frac{1}{2}$EC=$\frac{1}{2}$��4=2��cos30��=$\frac{DC}{EC}$��
��DC=EC•cos30��=4��$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$��
��AE=2DC-ED=4$\sqrt{3}$-2��
��S��AEC=$\frac{1}{2}$��AE��DC=$\frac{1}{2}$��4$\sqrt{3}$-2����2$\sqrt{3}$=12-2$\sqrt{3}$��
��2����ͼ2����A��AM��AH����FG��M��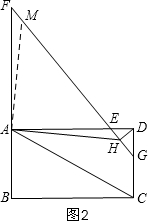
���MAH=��MAD+��DAH=90�㣬
�֡ߡ�FAD=��MAD+��FAM=90�㣬
���FAM=��DAH��
��AF��CD��
���F=��FGD
��DH��EG��
���DHE=��HDG+��FGD=90�㣬
��EDG=��EDH+��HDG=90�㣬
���FGD=��EDH��
���F=��EDH��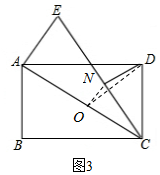
�֡�AF=2CD��AD=2CD��
��AF=AD��
���AFM�ա�ADH��
��AM=AH��FM=DH��
���MAH�ǵ���ֱ�������Σ�
��MH=$\sqrt{2}$AH��
��FH=MH+FM��
��FH=$\sqrt{2}$AH+DH��
��3����ͼ3��ʾ��ȡAC���е�O������ON��OD��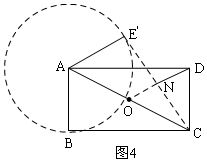
��AE=CD=4��
��AD=2CD=8��
��AC=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$��
��OD=2$\sqrt{5}$��
�ڡ�DON�У�
OD-ON��DN��OD+ON
��ON=$\frac{1}{2}$AE=2��
��2$\sqrt{5}$-2��DN��2$\sqrt{5}$+2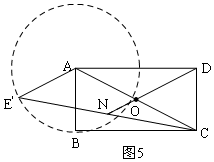
�ٵ���N���߶�DO��ʱ����ͼ4���߶�DNȡ��Сֵ��
��ON=$\frac{1}{2}$AE=2��
��DNmin=OD-ON=2$\sqrt{5}$-2��
�ڵ�N���߶�DO���ӳ�����ʱ����ͼ5���߶�DNȡ���ֵ��
��DNmax=OD+ON=2$\sqrt{5}$+2��
��0�㣼����360��
��2$\sqrt{5}$-2��DN��2$\sqrt{5}$+2��
���� �������ı��ε��ۺ��⣬�����˾��Ρ�ȫ�������Ρ���ֱ����������30��ǵ����ʣ������˵���ֱ��������ֱ�DZߺ�б�ߵĹ�ϵ���ڼ����߶�ȡֵ��Χʱ�����Էֱ�����߶ε����ֵ����Сֵ��Ȼ��д��ȡֵ��Χ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����һ���ӵ�ͬ����������ׯA��B������Ҫ�ں��Ϻ���һ�������ţ�������ʲô�ط�����ʹ�ŵ�����ľ���֮����̣�
��ͼ����һ���ӵ�ͬ����������ׯA��B������Ҫ�ں��Ϻ���һ�������ţ�������ʲô�ط�����ʹ�ŵ�����ľ���֮����̣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �˽�ij�����ݵ�ʹ��������� | B�� | �˽�ȫ��ͬѧÿ������������ʱ�� | ||
| C�� | ��ҵ��Ƹ����ӦƸ��Ա������ | D�� | ���ÿ��Ϸɻ��İ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 1 | C�� | 0.25 | D�� | 44026 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ֱ��m��n��Rt��ABC�Ķ���A��ֱ��n�ϣ���C=90�㣬����1=25�㣬��2=70�㣬���B=��������
��ͼ��ֱ��m��n��Rt��ABC�Ķ���A��ֱ��n�ϣ���C=90�㣬����1=25�㣬��2=70�㣬���B=��������| A�� | 65�� | B�� | 55�� | C�� | 45�� | D�� | 35�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ��ֱ��AB��CD�ڵ�O��OEƽ�֡�BOD��OFƽ�֡�COB����AOD����BOE=4��1�����AOF���ڣ�������
��ͼ��ʾ��ֱ��AB��CD�ڵ�O��OEƽ�֡�BOD��OFƽ�֡�COB����AOD����BOE=4��1�����AOF���ڣ�������| A�� | 130�� | B�� | 120�� | C�� | 110�� | D�� | 100�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x=0 | B�� | x=-1 | C�� | x=1 | D�� | x=2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com