
【题目】如图,已知AB∥CD,BC平分∠ABE,∠C=33°,则∠BED的度数是( )
A.16°
B.33°
C.49°
D.66°
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】如图,完成下列推理过程.
已知:DE⊥AO于E,BO⊥AO,∠CFB=∠EDO.
证明:CF∥DO.

证明:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°( )
∴DE∥BO( )
∴∠EDO=∠DOF( )
又∵∠CFB=∠EDO( ④ )
∴∠DOF=∠CFB( ⑤ )
∴CF∥DO( ⑥ )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生开展跳绳比赛活动,每班派5名学生参加,按团体总分多少排列名次,统计发现成绩最好的甲班和乙班总分相等,下表是甲班和乙班学生的比赛数据![]() 单位:个
单位:个![]()
选手 | 1号 | 2号 | 3号 | 4号 | 5号 | 总计 |
甲班 | 100 | 98 | 105 | 94 | 103 | 500 |
乙班 | 99 | 100 | 95 | 109 | 97 | 500 |
此时有学生建议,可以通过考察数据中的其他信息作为参考,请解答下列问题:
![]() 求两班比赛数据中的中位数,以及方差;
求两班比赛数据中的中位数,以及方差;
![]() 请根据以上数据,说明应该定哪一个班为冠军?为什么?
请根据以上数据,说明应该定哪一个班为冠军?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,AB=4,且∠ABC=∠ABE=60°,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则AM+BM+CM的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于某一函数给出如下定义:若存在实数p,当其自变量的值为p时,其函数值等于p,则称p为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差q称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度q为零.例如:下图中的函数有0,1两个不变值,其不变长度q等于1.
(1)分别判断函数y=x-1,y=x-1,y=x2有没有不变值?如果有,直接写出其不变长度;
(2)函数y=2x2-bx. ①若其不变长度为零,求b的值;
②若1≤b≤3,求其不变长度q的取值范围;
(3)记函数y=x2-2x(x≥m)的图象为G1 , 将G1沿x=m翻折后得到的函数图象记为G2 , 函数G的图象由G1和G2两部分组成,若其不变长度q满足0≤q≤3,则m的取值范围为.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )

A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,G是正方形形ABCD的边BC上一点,DE、BF分别垂直AG于点E、F,则图中与△ABF相似的三角形有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)请和两种不同的方法求图②中阴影部分的面积.
方法1:__方法2:___
(2)观察图②请你写出下列三个代数式;![]() mn之间的等量关系;
mn之间的等量关系;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:![]() 求
求![]() 的值.
的值.
②已知:![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校有一块长为(3a+b)m,宽为(2a+b)m的长方形空地,中间是边长(a+b)m的正方形草坪,其余为活动场地,学校计划将活动场地(阴影部分)进行硬化.
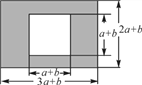
(1)用含a,b的代数式表示需要硬化的面积并化简;
(2)当a=5,b=2时,求需要硬化的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com