
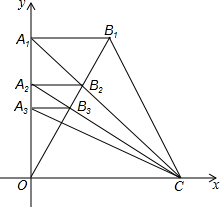
 在平面直角坐标系中,直角梯形OA1B1C的位置如图所示,A1的坐标为(0,2),点C的坐标为(2,0),tan∠OCB1=2,连接A1C交OB1于点B2,作A2B2⊥y轴于点A2,得到第二个直角梯形OA2B2C,连接A2C交OB1于点B3,同样办法得到第三个直角梯形OA3B3C,…以此类推,第n个直角梯形顶点Bn的坐标为($\frac{1}{12}$n2-$\frac{7}{12}$n+$\frac{3}{2}$,$\frac{1}{6}$n2-$\frac{7}{6}$n+3).
在平面直角坐标系中,直角梯形OA1B1C的位置如图所示,A1的坐标为(0,2),点C的坐标为(2,0),tan∠OCB1=2,连接A1C交OB1于点B2,作A2B2⊥y轴于点A2,得到第二个直角梯形OA2B2C,连接A2C交OB1于点B3,同样办法得到第三个直角梯形OA3B3C,…以此类推,第n个直角梯形顶点Bn的坐标为($\frac{1}{12}$n2-$\frac{7}{12}$n+$\frac{3}{2}$,$\frac{1}{6}$n2-$\frac{7}{6}$n+3). 分析 作B1D⊥OC于D,根据tan∠OCB1=2,求出B1的坐标,根据相似三角形的性质求出B2的坐标,总结规律得到答案.
解答 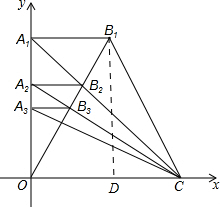 解:作B1D⊥OC于D,
解:作B1D⊥OC于D,
由题意得,B1D=OA1=2,0C=2,
∵tan∠OCB1=2,∴CD=1,
则AB1=1,B1(1,2),
∵A1B1∥OC,
∴$\frac{{A}_{1}{B}_{2}}{{B}_{2}C}$=$\frac{{A}_{1}{B}_{1}}{OC}$=$\frac{1}{2}$,
∵A2B2∥OC,
∴$\frac{{A}_{2}{B}_{2}}{OC}$=$\frac{{A}_{1}{B}_{2}}{{A}_{1}C}$=$\frac{{A}_{1}{A}_{2}}{{A}_{1}O}$=$\frac{1}{3}$,
∴A2B2=$\frac{2}{3}$,A2O=$\frac{4}{3}$,
则B2($\frac{2}{3}$,$\frac{4}{3}$),
同理,B3($\frac{1}{2}$,1),
…
Bn的坐标为:($\frac{1}{12}$n2-$\frac{7}{12}$n+$\frac{3}{2}$,$\frac{1}{6}$n2-$\frac{7}{6}$n+3)
点评 本题考查的是直角梯形的性质、坐标与图形的性质以及相似三角形的判定和性质,根据相似三角形的性质分别求出B1、B2、B3的坐标并总结出规律是解题的关键.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=180}\\{x=y•25%}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=180}\\{y=x•25%}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=180}\\{x-y=25%}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=180}\\{y-x=25%}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≥-1 | B. | a≤-1 | C. | a>-1 | D. | a<-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①④⑤ | B. | ③④⑤ | C. | ④⑤⑥ | D. | ②⑤⑥ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
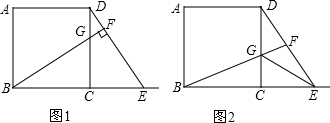
 如图,过△ABC的边BC的中点M作直线垂直于∠A的平分线AA′,且分别交直线AB,AC于点E,F,求证:BE=CF=$\frac{1}{2}$(AB-AC).
如图,过△ABC的边BC的中点M作直线垂直于∠A的平分线AA′,且分别交直线AB,AC于点E,F,求证:BE=CF=$\frac{1}{2}$(AB-AC).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+3y=17}\\{x=2y+1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+3y=17}\\{y=2x+1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y+3x=17}\\{x=2y+1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y+3x=17}\\{y=2x+1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2y-x)(x+2y) | B. | (x-2y)(-x-2y) | C. | (x-2y)(2y+x) | D. | (2y-x)(-x-2y) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
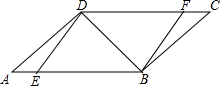 如图,在?ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
如图,在?ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com