
【题目】乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2两图的阴影部分面积,可以得到乘法公式 (用式子表达);
(4)运用你所得到的公式,计算下列各题:
①(2m+n-p)(2m-n+p);②10.3×9.7.

【答案】(1)a2 -b2;(2)a-b,a+b,(a+b)(a-b);(3)(a+b)(a﹣b)=a2 ﹣b2;(4)①4m2 -n2 +2np-p2;②99.91.
【解析】
(1)利用面积公式:大正方形的面积-小正方形的面积=阴影面积;
(2)根据图1可得矩形的长和宽,然后利用矩形面积公式进行求解即可;
(3)利用面积相等列出等式即可;
(4)①先分组,然后利用平方差公式简便计算即可;
②写成两个数的和与两个数的差的形式,然后利用平方差公式简便计算即可.
(1)利用正方形的面积公式可知:阴影部分的面积=a2 -b2,
故答案为:a2 -b2;
(2)由图可知矩形的宽是a-b,长是a+b,面积是(a+b)(a-b),
故答案为:a-b,a+b,(a+b)(a-b);
(3)由阴影部分的面积不变可得(a+b)(a﹣b)=a2 ﹣b2,
故答案为:(a+b)(a﹣b)=a2 ﹣b2;
(4)①原式=[2m+(n-p)][2m-(n-p)] =(2m)2 -(n-p)2 =4m2 -n2 +2np-p2;
②原式=(10+0.3)×(10-0.3)=102 -0.32=100-0.09=99.91.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,点A、点B均为格点.
(1)AB的长等于;
(2)若点C是以AB为底边的等腰直角三角形的顶点,点D在边AC上,且满足S△ABD= ![]() S△ABC . 请在如图所示的网格中,用无刻度的直尺,画出线段BD,并简要说明点D的位置时如何找到的(不要求证明). .
S△ABC . 请在如图所示的网格中,用无刻度的直尺,画出线段BD,并简要说明点D的位置时如何找到的(不要求证明). .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)某学校举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分(满分为10分):
方案1:所有评委所给分的平均数,
方案2:在所有评委所给分中,去掉一个最高分和一个最低分.然后再计算其余给分的l平均数.
方案3:所有评委所给分的中位效.
方案4:所有评委所给分的众数.
为了探究上述方案的合理性.先对某个同学的演讲成绩进行了统计实验.下面是这个同学的得分统计图:

(1)分别按上述4个方案计算这个同学演讲的最后得分;
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适台作为这个同学演讲的最后得分,并给出该同学的最后得分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.
(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;
(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大?若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )

A. 110° B. 120° C. 130° D. 140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年宁波市北仑区体育中考的3个选测项目分别是50米跑,一分钟跳绳,篮球运球投篮.另规定:游泳满分的学生,只需从3个选测项目中选择一项进行测试;游泳未得满分或未参加的学生,需从3个选测项目中任选两项进行测试.
(1)小明因游泳测试获得了满分,求他在3个选测项目中选择“一分钟跳绳”项目的概率.
(2)若小红和小慧的游泳测试都未得满分,她们都必须从3个选测项目中选择两项进行体育中考测试,请用列表(或画树状图)的方法,求出小红和小慧选择的两个项目完全相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD,线段CD分别表示该产品每千克生产成本y1(单位:元),销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.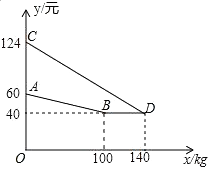
(1)请解释图中点D的实际意义.
(2)求线段CD所表示的y2与x之间的函数表达式.
(3)当该产品产量为多少时,获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李克强总理连续三年把“全民阅读”写入《政府工作报告》,足以说明阅读的重要性.某校为了解学生最喜爱的书籍的类型,随机抽取了部分学生进行调查,并绘制了如下的条形统计图(部分信息未给出).已知,这些学生中有15%的人喜欢漫画,喜欢小说名著的人数是喜欢童话的 ![]() ,请完成下列问题:
,请完成下列问题:
(1)求本次抽取的学生人数;
(2)喜欢小说名著、喜欢童话故事的学生各有多少人?并补全条形统计图;
(3)全校共有2100名学生,请估计最喜欢“小说名著”的人数有多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com