
 如图,为了测量矗立在高速公路水平地面上的交通警示牌的高度CD,在距M相距4米的A处,测得警示牌下端D的仰角为45°,再笔直往前走8米到达B处,在B处测得警示牌上端C的仰角为30°,求警示牌的高度CD.(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,为了测量矗立在高速公路水平地面上的交通警示牌的高度CD,在距M相距4米的A处,测得警示牌下端D的仰角为45°,再笔直往前走8米到达B处,在B处测得警示牌上端C的仰角为30°,求警示牌的高度CD.(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)  黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:选择题
| 年人均收入 | 2 | 3 | 4 | 5 | 6 |
| 村庄个数 | 2 | 1 | 2 | 3 | 1 |
| A. | 4、3 | B. | 4、4 | C. | 5、4 | D. | 5、5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
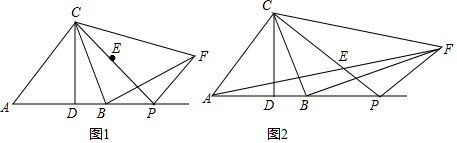
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 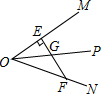 | B. | 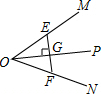 | C. | 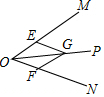 | D. | 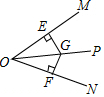 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
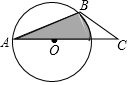 如图,AB为⊙O的弦,⊙O的切线BC与射线AO交于点C,若∠C=45°,⊙O的半径为6,则图中阴影部分的面积等于( )
如图,AB为⊙O的弦,⊙O的切线BC与射线AO交于点C,若∠C=45°,⊙O的半径为6,则图中阴影部分的面积等于( )| A. | 18$\sqrt{2}$+9π | B. | 9$\sqrt{2}$+4.5π | C. | 9$\sqrt{2}$+9π | D. | $\frac{9}{2}$$\sqrt{2}$+4.5π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com