
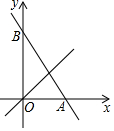 如图,一次函数y=-$\sqrt{3}$x+$\sqrt{3}$的图象与x轴、y轴交于A、B两点,P为一次函数y=x的图象上一点,以P为圆心能够画出圆与直线AB和y轴同时相切,则∠BPO=30°或120°.
如图,一次函数y=-$\sqrt{3}$x+$\sqrt{3}$的图象与x轴、y轴交于A、B两点,P为一次函数y=x的图象上一点,以P为圆心能够画出圆与直线AB和y轴同时相切,则∠BPO=30°或120°. 分析 首先利用三角函数求得∠OBA的度数,然后分成P在AB的左侧和右侧两种情况进行讨论,利用切线长定理以及三角形的内角和定理即可求解.
解答 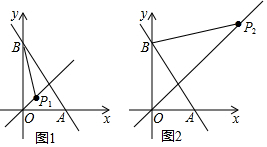 解:在y=-$\sqrt{3}$x+$\sqrt{3}$中,当x=0时,y=$\sqrt{3}$,则B的坐标是(0,$\sqrt{3}$);
解:在y=-$\sqrt{3}$x+$\sqrt{3}$中,当x=0时,y=$\sqrt{3}$,则B的坐标是(0,$\sqrt{3}$);
当y=0时,x=1,则A的坐标是(1,0);
则tan∠OBA=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
则∠OBA=30°.
当P在AB的左侧时,此时P一定在直角△OAB的内部.
如图1的位置:∵直线y=x时第一、三象限的角的平分线,
∴∠BOP1=45°,
∵OB和AB是圆切线,
∴∠OBP1=$\frac{1}{2}$∠OBA=$\frac{1}{2}$×30°=15°,
∴∠BP1O=180°-15°-45°=120°;
当P在AB的右侧时,如图2,
同理可得∠ABP2=$\frac{1}{2}$(180°-∠OBA)=$\frac{1}{2}$×(180°-30°)=75°,
∠BOP2=45°,
∴∠BP2O=180°-75°-45°=30°.
故答案是:30°或120°.
点评 本题考查了切线长定理,以及三角形的内角和的应用,正确对P的位置进行讨论是关键.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 4x-x=3 | B. | (3x2)3=9x6 | C. | (x+2)(x-2)=x2-4 | D. | $\sqrt{6}$÷$\sqrt{3}$=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
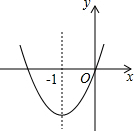 如图,已知经过原点的抛物线y-ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:①ab>0,②a+b+c>0,③当-2<x<0时,y<0,正确的结论是①②③.
如图,已知经过原点的抛物线y-ax2+bx+c(a≠0)的对称轴是直线x=-1,下列结论中:①ab>0,②a+b+c>0,③当-2<x<0时,y<0,正确的结论是①②③.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com