
 DC.若AB=10,BC=12,则图中阴影部分的面积为 .
DC.若AB=10,BC=12,则图中阴影部分的面积为 .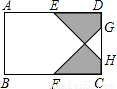
 DC,可得相似比,那么可求出NM,MQ,以及EF,CD的长,再利用三角形的面积公式可求出△EFM和△MGH的面积,用矩形EFCD的面积减去△EFM的面积减去△GHM的面积,即可求阴影部分面积.
DC,可得相似比,那么可求出NM,MQ,以及EF,CD的长,再利用三角形的面积公式可求出△EFM和△MGH的面积,用矩形EFCD的面积减去△EFM的面积减去△GHM的面积,即可求阴影部分面积. 解:连接EF,过M作MQ⊥EF,交EF于N,交CD于Q,
解:连接EF,过M作MQ⊥EF,交EF于N,交CD于Q, •BC=6,
•BC=6, ×10×4=20,
×10×4=20, ×5×2=5,S矩形EFCD=6×10=60,
×5×2=5,S矩形EFCD=6×10=60,

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源:2010年山东省泰安市新泰市中考数学模拟试卷(一)(解析版) 题型:填空题
 DC.若AB=10,BC=12,则图中阴影部分的面积为 .
DC.若AB=10,BC=12,则图中阴影部分的面积为 .
查看答案和解析>>
科目:初中数学 来源:2009年河北省承德市中考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2009年河北省承德市中考数学一模试卷(解析版) 题型:解答题
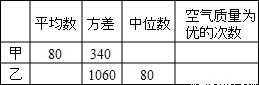
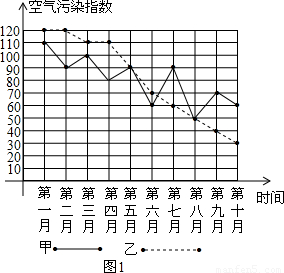
查看答案和解析>>
科目:初中数学 来源:2009年河北省承德市中考数学一模试卷(解析版) 题型:填空题
 DC.若AB=10,BC=12,则图中阴影部分的面积为 .
DC.若AB=10,BC=12,则图中阴影部分的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com