
【题目】解方程:
(1) ![]() =0;
=0;
(2) ![]() -1.
-1.
【答案】(1)x=0;(2)x=-![]()
【解析】试题分析:
(1)方程两边乘以最简公分母(x+1)(x-1),把分式方程转化为整式方程求解,再按照解一元一次方程的方法进行求解,最后进行检验;
(2) 方程两边乘以最简公分母(x-2)(x+3),把分式方程转化为整式方程求解,再按照解一元一次方程的方法进行求解,最后进行检验.
试题解析:
解 (1)方程两边都乘(x+1)(x-1),得
3(x+1)-(x+3)=0,
3x+3-x-3=0,
2x=0,x=0.
检验:将x=0代入原方程,得左边=0=右边.
所以x=0是原方程的解.
(2)方程两边同乘(x-2)(x+3),得
6(x+3)=x(x-2)-(x-2)(x+3).
化简,得9x=-12,解得x=-![]() .
.
当x=-![]() 时,(x-2)(x+3)≠0,
时,(x-2)(x+3)≠0,
故x=-![]() 是原方程的解.
是原方程的解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
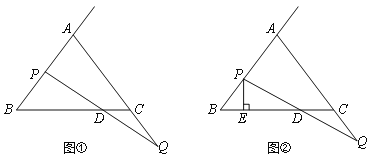
【题目】已知△ABC中,AB=AC=BC=6.点P射线BA上一点,点Q是AC的延长线上一点,且BP=CQ,连接PQ,与直线BC相交于点D.
(1)如图①,当点P为AB的中点时,求CD的长;
(2)如图②,过点P作直线BC的垂线,垂足为E,当点P,Q分别在射线BA和AC的延长线上任意地移动过程中,线段BE,DE,CD中是否存在长度保持不变的线段?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
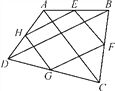
【题目】如图所示,E,F,G,H分别是四边形ABCD的边AB,BC,CD,AD的中点.
(1)当四边形ABCD是矩形时,四边形EFGH是_________,请说明理由;
(2)当四边形ABCD满足什么条件时,四边形EFGH为正方形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件B种产品需用甲种原料4千克、乙种原料10千克,可获利润1200元。设生产A种产品的生产件数为x, A、B两种产品所获总利润为y (元)
(1)试写出y与x之间的函数关系式;
(2)求出自变量x的取值范围;
(3)利用函数的性质说明哪种生产方案获总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN,EF是两面互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,则∠1=∠2.
(1)用尺规作图作出镜面BC经镜面EF反射后的反射光线CD;
(2)试判断AB与CD的位置关系;
(3)你是如何思考的?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,- ![]() )三点.
)三点.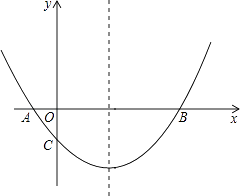
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一副直角三角板放在同一条直线AB上,其中![]() ,
,![]() .
.
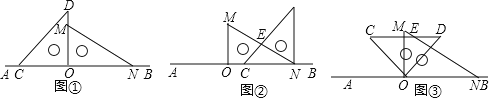
![]() 将图1中的三角尺OCD沿AB的方向平移至图
将图1中的三角尺OCD沿AB的方向平移至图![]() 的位置,使得点O与点N重合,CD与MN相交于点E,求
的位置,使得点O与点N重合,CD与MN相交于点E,求![]() 的度数;
的度数;
![]() 将图1中的三角尺OCD绕点O按顺时针方向旋转,使一边OD在
将图1中的三角尺OCD绕点O按顺时针方向旋转,使一边OD在![]() 的内部,如图3,且OD恰好平分
的内部,如图3,且OD恰好平分![]() ,CD与MN相交于点E,求
,CD与MN相交于点E,求![]() 的度数;
的度数;
![]() 将图1中的三角尺OCD绕点O按每秒
将图1中的三角尺OCD绕点O按每秒![]() 的速度沿顺时针方向旋转一周,在旋转的过程中,在第______ 秒时,边CD恰好与边MN平行;在第______ 秒时,直线CD恰好与直线MN垂直
的速度沿顺时针方向旋转一周,在旋转的过程中,在第______ 秒时,边CD恰好与边MN平行;在第______ 秒时,直线CD恰好与直线MN垂直![]() 直接写出结果
直接写出结果![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
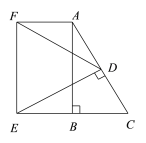
【题目】Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,从D作DE⊥AC与CB的延长线交于点E,以AB、BE为邻边作矩形ABEF,连结DF,则DF的长是( )
A. 4![]() B. 3
B. 3![]() C. 2
C. 2![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自行车队进行训练,训练时所有队员都以相同的速度前进,突然,1号队员以每小时比其他队员快10千米的速度独自行进,行进了10千米后掉转车头,速度不变往回骑,直到与其他的队员会合.从1号队员离队开始到与其他队员重新会合,经过了15分钟.
(1)其他队员的行进速度是多少?
(2)1号队员从离队开始到与队员重新会合这个过程中,经过多长时间与其他队员相距1千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com