
ČēĶ¼£¬ŅŃÖŖÖ±Ļß ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćB£¬½«”÷AOBČʵćOĖ³Ź±ÕėŠż×Ŗ90”ćŗóµĆµ½”÷COD£®
ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćB£¬½«”÷AOBČʵćOĖ³Ź±ÕėŠż×Ŗ90”ćŗóµĆµ½”÷COD£®
£Ø1£©µćCµÄ×ų±źŹĒ”” ””£¬Ļ߶ĪADµÄ³¤µČÓŚ”” ””£»
£Ø2£©µćMŌŚCDÉĻ£¬ĒŅCM=OM£¬Å×ĪļĻßy=x2+bx+c¾¹żµćG£¬M£¬ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø3£©Čē¹ūµćEŌŚyÖįÉĻ£¬ĒŅĪ»ÓŚµćCµÄĻĀ·½£¬µćFŌŚÖ±ĻßACÉĻ£¬ÄĒĆ“ŌŚ£Ø2£©ÖŠµÄÅ×ĪļĻßÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹µĆŅŌC£¬E£¬F£¬PĪŖ¶„µćµÄĖıߊĪŹĒĮāŠĪ£æČō“ęŌŚ£¬ĒėĒó³öøĆĮāŠĪµÄÖܳ¤l£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
½ā£ŗ£Ø1£©£Ø0£¬3£©£»4”£
£Ø2£©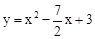
£Ø3£©Å×ĪļĻßÉĻ“ęŌŚµćP£¬Ź¹µĆŅŌC£¬E£¬F£¬PĪŖ¶„µćµÄĖıߊĪŹĒĮāŠĪ”£
½āĪöŹŌĢā·ÖĪö£ŗ£Ø1£©Ź×ĻČĒó³öĶ¼ĻóÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćBµÄ×ų±ź£¬½ų¶ųµĆ³öCµć×ų±źŅŌ¼°Ļ߶ĪADµÄ³¤£ŗ
”ß ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćB£¬
ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćB£¬
”ąy=0Ź±£¬x=©3£¬x=0Ź±£¬y=1”£
”ąAµć×ų±źĪŖ£ŗ£Ø©3£¬0£©£¬Bµć×ų±źĪŖ£ŗ£Ø0£¬1£©”£
”ąOC=3£¬DO=1”£
”ąµćCµÄ×ų±źŹĒ£Ø0£¬3£©£¬Ļ߶ĪADµÄ³¤µČÓŚ4”£
£Ø2£©Ź×ĻČµĆ³öµćMŹĒCDµÄÖŠµć£¬¼“æÉµĆ³öMµć×ų±ź£¬½ų¶ųĄūÓĆ“ż¶ØĻµŹż·ØĒ󶞓ĪŗÆŹż½āĪöŹ½”£
”ßCM=OM£¬”ą”ĻOCM=”ĻCOM”£
”ß”ĻOCM+”ĻODM=”ĻCOM+”ĻMOD=90”ć£¬”ą”ĻODM=”ĻMOD”£”ąOM=MD=CM”£
”ąµćMŹĒCDµÄÖŠµć£¬”ąµćMµÄ×ų±źĪŖ£Ø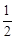 £¬
£¬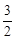 £©”£
£©”£
”ßÅ×ĪļĻßy=x2+bx+c¾¹żµćC£¬M£¬
”ą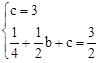 £¬½āµĆ£ŗ
£¬½āµĆ£ŗ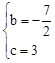 ”£
ӣ
”ąÅ×ĪļĻßy=x2+bx+cµÄ½āĪöŹ½ĪŖ£ŗ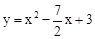 ”£
ӣ
£Ø3£©·Ö±šøł¾Żµ±µćFŌŚµćCµÄ×ó±ßŹ±ŅŌ¼°µ±µćFŌŚµćCµÄÓŅ±ßŹ±£¬·ÖĪöĖıߊĪCFPEĪŖĮāŠĪµĆ³ö¼“æÉ”£
ĒéŠĪ1£ŗČēĶ¼1£¬µ±µćFŌŚµćCµÄ×ó±ßŹ±£¬ĖıߊĪCFEPĪŖĮāŠĪ£¬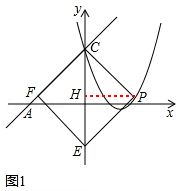
”ą”ĻFCE=PCE”£
ÓÉĢāŅāæÉÖŖ£¬OA=OC£¬”ą”ĻACO=”ĻPCE=45”ć”£
”ą”ĻFCP=90”ć”£”ąĮāŠĪCFEPĪŖÕż·½ŠĪ”£
¹żµćP×÷PH”ĶCE£¬“¹×ćĪŖH£¬
ŌņRt”÷CHPĪŖµČŃüÖ±½ĒČż½ĒŠĪ”£
”ąCP=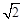 CH=
CH=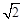 PHӣ
PHӣ
ÉčµćPĪŖ£Øx£¬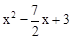 £©£¬ŌņOH=
£©£¬ŌņOH=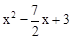 £¬PH=x£¬
£¬PH=x£¬
”ßPH=CH=OC©OH£¬”ą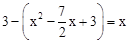 £¬½āµĆ£ŗx1=
£¬½āµĆ£ŗx1=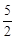 £¬ x2=0£ØÉįČ„£©”£
£¬ x2=0£ØÉįČ„£©”£
”ąCP=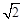 CH=
CH= ӣ
ӣ
”ąĮāŠĪCFEPµÄÖܳ¤lĪŖ£ŗ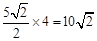 ”£
ӣ
ĒéŠĪ2£ŗČēĶ¼2£¬µ±µćFŌŚµćCµÄÓŅ±ßŹ±£¬ĖıߊĪCFPEĪŖĮāŠĪ£¬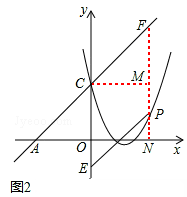
”ąCF=PF£¬CE”ĪFP”£
”ßÖ±ĻßAC¹żµćA£Ø©3£¬0£©£¬µćC£Ø0£¬3£©£¬
”ąÖ±ĻßACµÄ½āĪöŹ½ĪŖ£ŗy=x+3”£
¹żµćC×÷CM”ĶPF£¬“¹×ćĪŖM£¬
ŌņRt”÷CMFĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬CM=FM”£
ŃÓ³¤PF½»xÖįÓŚµćN£¬ŌņPN”ĶxÖį£¬
”ąPF=FN©PN”£
ÉčµćPĪŖ£Øx£¬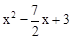 £©£¬ŌņµćFĪŖ£Øx£¬x+3£©£¬
£©£¬ŌņµćFĪŖ£Øx£¬x+3£©£¬
”ą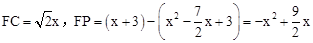 ”£
ӣ
”ą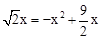 £¬½āµĆ£ŗ
£¬½āµĆ£ŗ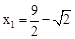 £¬x2=0£ØÉįČ„£©”£
£¬x2=0£ØÉįČ„£©”£
”ą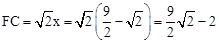 ”£
ӣ
”ąĮāŠĪCFEPµÄÖܳ¤lĪŖ£ŗ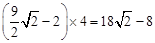 £©”£
£©”£
×ŪÉĻĖłŹö£¬ÕāŃłµÄĮāŠĪ“ęŌŚ£¬ĖüµÄÖܳ¤ĪŖ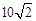 »ņ
»ņ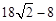 ”£
ӣ



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
ČēĶ¼£¬ŌŚµČ±ß”÷ABCÖŠ£¬AB=3£¬D”¢E·Ö±šŹĒAB”¢ACÉĻµÄµć£¬ĒŅDE”ĪBC£¬½«”÷ADEŃŲDE·ÕŪ£¬ÓėĢŻŠĪBCEDÖŲµžµÄ²æ·Ö¼Ē×÷Ķ¼ŠĪL£®
£Ø1£©Ēó”÷ABCµÄĆ껿£»
£Ø2£©ÉčAD=x£¬Ķ¼ŠĪLµÄĆ껿ĪŖy£¬Ēóy¹ŲÓŚxµÄŗÆŹż½āĪöŹ½£»
£Ø3£©ŅŃÖŖĶ¼ŠĪLµÄ¶„µć¾łŌŚ”ŃOÉĻ£¬µ±Ķ¼ŠĪLµÄĆ껿×ī“óŹ±£¬Ēó”ŃOµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ņ»øö¶ž“ĪŗÆŹżµÄĶ¼Ļó¾¹żµćA£Ø1£¬0£©”¢B£Ø3£¬0£©Į½µć£®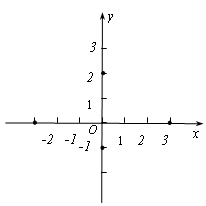
£Ø1£©Š“³öÕāøö¶ž“ĪŗÆŹżµÄ¶Ō³ĘÖį£»
£Ø2£©ÉčÕāøö¶ž“ĪŗÆŹżµÄ¶„µćĪŖD£¬ÓėyÖį½»ÓŚµćC£¬ĖüµÄ¶Ō³ĘÖįÓėxÖį½»ÓŚµćE£¬Į¬½ÓAD”¢DEŗĶDB£¬µ±”÷AOCÓė”÷DEBĻąĖĘŹ±£¬ĒóÕāøö¶ž“ĪŗÆŹżµÄ±ķ“ļŹ½”£
[ĢįŹ¾£ŗČē¹ūŅ»øö¶ž“ĪŗÆŹżµÄĶ¼ĻóÓėxÖįµÄ½»µćĪŖ A£¬ÄĒĆ“ĖüµÄ±ķ“ļŹ½æɱķŹ¾ĪŖ£ŗ
A£¬ÄĒĆ“ĖüµÄ±ķ“ļŹ½æɱķŹ¾ĪŖ£ŗ ]
]
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
ČēĶ¼£¬”÷ABCÖŠ£¬AB=BC£¬AC=8£¬tanA=k£¬PĪŖAC±ßÉĻŅ»¶Æµć£¬ÉčPC=x£¬×÷PE”ĪAB½»BCÓŚE£¬PF”ĪBC½»ABÓŚF£®
£Ø1£©Ö¤Ć÷£ŗ”÷PCEŹĒµČŃüČż½ĒŠĪ£»
£Ø2£©EM”¢FN”¢BH·Ö±šŹĒ”÷PEC”¢”÷AFP”¢”÷ABCµÄøߣ¬ÓĆŗ¬xŗĶkµÄ“śŹżŹ½±ķŹ¾EM”¢FN£¬²¢Ģ½¾æEM”¢FN”¢BHÖ®¼äµÄŹżĮæ¹ŲĻµ£»
£Ø3£©µ±k=4Ź±£¬ĒóĖıߊĪPEBFµÄĆ껿SÓėxµÄŗÆŹż¹ŲĻµŹ½£®xĪŖŗĪÖµŹ±£¬SÓŠ×ī“óÖµ£æ²¢Ēó³öSµÄ×ī“óÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
ČēĶ¼£¬ŅŃÖŖÅ×ĪļĻß ÓėxÖįĻą½»ÓŚA”¢BĮ½µć£¬ÓėyÖįĻą½»ÓŚµćC£¬ČōŅŃÖŖAµćµÄ×ų±źĪŖA£Ø©2£¬0£©£®
ÓėxÖįĻą½»ÓŚA”¢BĮ½µć£¬ÓėyÖįĻą½»ÓŚµćC£¬ČōŅŃÖŖAµćµÄ×ų±źĪŖA£Ø©2£¬0£©£®
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½¼°ĖüµÄ¶Ō³ĘÖį·½³Ģ£»
£Ø2£©ĒóµćCµÄ×ų±ź£¬Į¬½ÓAC”¢BC²¢ĒóĻ߶ĪBCĖłŌŚÖ±ĻߵĽāĪöŹ½£»
£Ø3£©ŹŌÅŠ¶Ļ”÷AOCÓė”÷COBŹĒ·ńĻąĖĘ£æ²¢ĖµĆ÷ĄķÓÉ£»
£Ø4£©ŌŚÅ×ĪļĻߵĶŌ³ĘÖįÉĻŹĒ·ń“ęŌŚµćQ£¬Ź¹”÷ACQĪŖµČŃüČż½ĒŠĪ£æČō²»“ęŌŚ£¬Ēó³ö·ūŗĻĢõ¼žµÄQµć×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
ŅŃÖŖ£ŗÖ±Ļß ¹żÅ×ĪļĻß
¹żÅ×ĪļĻß µÄ¶„µćP£¬ČēĶ¼ĖłŹ¾£®
µÄ¶„µćP£¬ČēĶ¼ĖłŹ¾£®
£Ø1£©¶„µćPµÄ×ų±źŹĒ”” ””£»
£Ø2£©ČōÖ±Ļßy=ax+b¾¹żĮķŅ»µćA£Ø0£¬11£©£¬Ēó³öøĆÖ±Ļߵıķ“ļŹ½£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬ČōÓŠŅ»ĢõÖ±Ļßy=mx+nÓėÖ±Ļßy=ax+b¹ŲÓŚxÖį³ÉÖį¶Ō³Ę£¬ĒóÖ±Ļßy=mx+nÓėÅ×ĪļĻß µÄ½»µć×ų±ź£®
µÄ½»µć×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
£Ø2013ÄźÕć½ŅåĪŚ10·Ö£©ĪŖÓ½ÓÖŠ¹śÉ²©»į£¬Ä³ÉĢ¼Ņ¼Ę»®“Ó³§¼Ņ²É¹ŗA£¬BĮ½ÖÖ²śĘ·¹²20¼ž£¬²śĘ·µÄ²É¹ŗµ„¼Ū£ØŌŖ/¼ž£©ŹĒ²É¹ŗŹżĮæ£Ø¼ž£©µÄŅ»“ĪŗÆŹż£®ĻĀ±ķĢį¹©ĮĖ²æ·Ö²É¹ŗŹż¾Ż£®
| ²É¹ŗŹżĮæ£Ø¼ž£© | 1 | 2 | ” |
| A²śĘ·µ„¼Ū£ØŌŖ/¼ž£© | 1480 | 1460 | ” |
| B²śĘ·µ„¼Ū£ØŌŖ/¼ž£© | 1290 | 1280 | ” |
 £¬ĒŅA²śĘ·²É¹ŗµ„¼Ū²»µĶÓŚ1200ŌŖ£®ĒóøĆÉĢ¼Ņ¹²ÓŠ¼øÖÖ½ų»õ·½°ø£»
£¬ĒŅA²śĘ·²É¹ŗµ„¼Ū²»µĶÓŚ1200ŌŖ£®ĒóøĆÉĢ¼Ņ¹²ÓŠ¼øÖÖ½ų»õ·½°ø£»²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
Ö±Ļß Óėx”¢yÖį·Ö±š½»ÓŚµćA”¢C£®Å×ĪļĻßµÄĶ¼Ļó¾¹żA”¢CŗĶµćB£Ø1£¬0£©£®
Óėx”¢yÖį·Ö±š½»ÓŚµćA”¢C£®Å×ĪļĻßµÄĶ¼Ļó¾¹żA”¢CŗĶµćB£Ø1£¬0£©£®
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ŌŚÖ±ĻßACÉĻ·½µÄÅ×ĪļĻßÉĻÓŠŅ»¶ÆµćD£¬µ±DÓėÖ±ĻßACµÄ¾ąĄėDE×ī“óŹ±£¬Ēó³öµćDµÄ×ų±ź£¬²¢Ēó³ö×ī“ó¾ąĄėŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
ČēĶ¼¢Ł£¬Čō¶ž“ĪŗÆŹż µÄĶ¼ĻóÓė£ųÖį½»ÓŚµćA£Ø£2,0£©,B£Ø3,0£©Į½µć£¬µćA¹ŲÓŚÕż±ČĄżŗÆŹż
µÄĶ¼ĻóÓė£ųÖį½»ÓŚµćA£Ø£2,0£©,B£Ø3,0£©Į½µć£¬µćA¹ŲÓŚÕż±ČĄżŗÆŹż µÄĶ¼ĻóµÄ¶Ō³ĘµćĪŖC”£
µÄĶ¼ĻóµÄ¶Ō³ĘµćĪŖC”£
£Ø1£©Ēób”¢cµÄÖµ£»
£Ø2£©Ö¤Ć÷£ŗµćC ŌŚĖłĒóµÄ¶ž“ĪŗÆŹżµÄĶ¼ĻóÉĻ£»
£Ø3£©ČēĶ¼¢Ś£¬¹żµćB×÷DB”Ķ£ųÖį½»Õż±ČĄżŗÆŹż µÄĶ¼ĻóÓŚµćD£¬Į¬½įAC£¬½»Õż±ČĄżŗÆŹż
µÄĶ¼ĻóÓŚµćD£¬Į¬½įAC£¬½»Õż±ČĄżŗÆŹż µÄĶ¼ĻóÓŚµćE£¬Į¬½įAD”¢CD”£Čē¹ū¶ÆµćP“ÓµćAŃŲĻ߶ĪAD·½ĻņŅŌĆæĆė2øöµ„Ī»µÄĖŁ¶ČĻņµćDŌĖ¶Æ£¬Ķ¬Ź±¶ÆµćQ“ÓµćDŃŲĻ߶ĪDC·½ĻņŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņµćCŌĖ¶Æ£¬µ±ĘäÖŠŅ»øöµ½“ļÖÕµćŹ±£¬ĮķŅ»øöĖęÖ®Ķ£Ö¹ŌĖ¶Æ£¬Į¬½įPQ”¢QE”¢PE£¬ÉčŌĖ¶ÆŹ±¼äĪŖtĆė£¬ŹĒ·ń“ęŌŚÄ³Ņ»Ź±æĢ£¬Ź¹PEĘ½·Ö”ĻAPQ£¬Ķ¬Ź±QEĘ½·Ö”ĻPQC£¬Čō“ęŌŚ£¬Ēó³ötµÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ”£
µÄĶ¼ĻóÓŚµćE£¬Į¬½įAD”¢CD”£Čē¹ū¶ÆµćP“ÓµćAŃŲĻ߶ĪAD·½ĻņŅŌĆæĆė2øöµ„Ī»µÄĖŁ¶ČĻņµćDŌĖ¶Æ£¬Ķ¬Ź±¶ÆµćQ“ÓµćDŃŲĻ߶ĪDC·½ĻņŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČĻņµćCŌĖ¶Æ£¬µ±ĘäÖŠŅ»øöµ½“ļÖÕµćŹ±£¬ĮķŅ»øöĖęÖ®Ķ£Ö¹ŌĖ¶Æ£¬Į¬½įPQ”¢QE”¢PE£¬ÉčŌĖ¶ÆŹ±¼äĪŖtĆė£¬ŹĒ·ń“ęŌŚÄ³Ņ»Ź±æĢ£¬Ź¹PEĘ½·Ö”ĻAPQ£¬Ķ¬Ź±QEĘ½·Ö”ĻPQC£¬Čō“ęŌŚ£¬Ēó³ötµÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ”£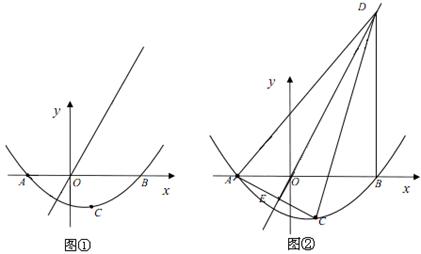
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com