
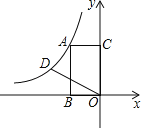
【题目】如图,矩形ABOC的顶点B、C分别在x轴,y轴上,顶点A在第二象限,点B的坐标为(﹣2,0).将线段OC绕点O逆时针旋转60°至线段OD,若反比例函数y=![]() (k≠0)的图象经过A、D两点,则k值为______.
(k≠0)的图象经过A、D两点,则k值为______.
科目:初中数学 来源: 题型:
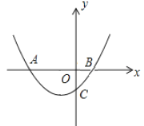
【题目】如图,已知抛物线![]() 交x轴于A(-4,0),B两点,交y轴于点C(0,-2).
交x轴于A(-4,0),B两点,交y轴于点C(0,-2).
(1)求抛物线的解析式;
(2)过点M(m,0)(-4<m<0)且垂直于x轴的直线与抛物线![]() 相交于点N,求线段OM+MN的最大值.
相交于点N,求线段OM+MN的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是弧![]() 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
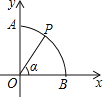
A. (sinα,sinα) B. (cosα,cosα) C. (cosα,sinα) D. (sinα,cosα)
查看答案和解析>>
科目:初中数学 来源: 题型:
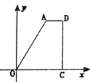
【题目】如图,在四边形![]() 中,O为坐标原点,
中,O为坐标原点,![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() 垂直于
垂直于![]() 轴,
轴,![]() ,
,![]() .若动点
.若动点![]() 、
、![]() 同时从点0出发,
同时从点0出发,![]() 点沿折线
点沿折线![]() 运动,到达
运动,到达![]() 点时停止;
点时停止;![]() 点沿
点沿![]() 运动,到达
运动,到达![]() 点时停止,它们运动的速度都是每秒1个单位长度。设
点时停止,它们运动的速度都是每秒1个单位长度。设![]() 运动
运动![]() 秒时,
秒时,![]() 的面积为
的面积为![]() (平方单位),则
(平方单位),则![]() 关于
关于![]() 的函数图象大致为( )
的函数图象大致为( )
A.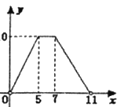 B.
B.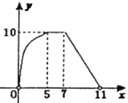
C.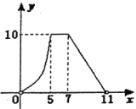
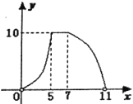
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() (
(![]() 左
左![]() 右)两点,交
右)两点,交![]() 轴于点
轴于点![]() ,且
,且![]() .
.
(1)如图(1)求抛物线的解析式;
(2)如图(2)![]() 为第四象限抛物线上一点,连接
为第四象限抛物线上一点,连接![]() ,将线段
,将线段![]() 沿着
沿着![]() 轴翻折,得到线段
轴翻折,得到线段![]() ,连接
,连接![]() ,设
,设![]() 点的横坐标为
点的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)如图(3)在(2)的条件下,![]() 是第一象限抛物线上的一点,
是第一象限抛物线上的一点,![]() 轴交
轴交![]() 的延长线于
的延长线于![]() ,垂足是
,垂足是![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 轴于
轴于![]() 、交直线
、交直线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
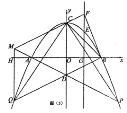
【题目】(2013年四川自贡12分)将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.

(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图②中,若AP1=2,则CQ等于多少?
(3)如图③,在B1C上取一点E,连接BE、P1E,设BC=1,当BE⊥P1B时,求△P1BE面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探究发现:下面是一道例题及解答过程,请补充完整:
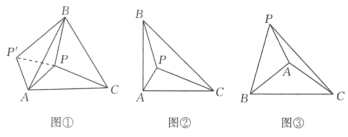
如图①在等边△ABC内部,有一点P,若∠APB=150°,求证:AP2+BP2=CP2
证明:将△APC绕A点逆时针旋转60°,得到△AP’B,连接PP’,则△APP’为等边三角形
∴∠APP’=60° ,PA=PP’ ,PC=
∵∠APB=150°,∴∠BPP’=90°
∴P’P2+BP2= ,即PA2+PB2=PC2
(2)类比延伸:如图②在等腰△ABC中,∠BAC=90°,内部有一点P,若∠APB=135°,试判断线段PA,PB,PC之间的数量关系,并证明.
(3)联想拓展:如图③在△ABC中,∠BAC=120°,AB=AC,点P在直线AB上方,且∠APB=60°,满足(kPA)2+PB2=PC2(其中k>0),请直接写出k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
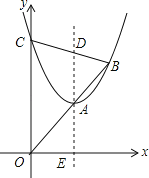
【题目】如图,抛物线y=x2+bx+c(c>0)与y轴交于点C,顶点为A,抛物线的对称轴交x轴于点E,交BC于点D,tan∠AOE=![]() .直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是_____.
.直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,则下列结论中正确的有( )
(1)若通话时间少于120分,则A方案比B方案便宜20元;
(2)若通话时间超过200分,则B方案比A方案便宜12元;
(3)若通讯费用为60元,则B方案比A方案的通话时间多;
(4)若两种方案通讯费用相差10元,则通话时间是145分或185分.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com