
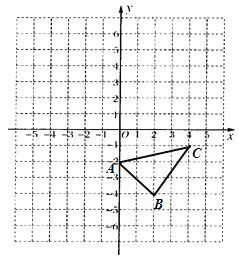
【题目】如图,直角坐标系xOy中,一次函数![]() 的图象
的图象![]() 分别与x,y轴交于A,B两点,正比例函数的图象
分别与x,y轴交于A,B两点,正比例函数的图象![]() 与
与![]() 交于点C(m,3),
交于点C(m,3),

(1)求m的值及![]() 的解析式;
的解析式;
(2)求![]() 的值.
的值.
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中.
(1)作出△ABC关于![]() 轴对称的
轴对称的![]() ,并写出
,并写出![]() 三个顶点的坐标:
三个顶点的坐标: ![]() ( ),
( ),![]() ( ),
( ),![]() ( );
( );
(2)直接写出△ABC的面积为 ;
(3)在![]() 轴上画点P,使PA+PC最小.
轴上画点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D,E,F,G,H为⊙O的八等分点,AD与BH的交点为I,若⊙O的半径为1,则HI的长等于( )
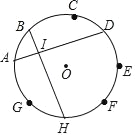
A. 2﹣![]() B. 2+
B. 2+ ![]() C. 2
C. 2![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
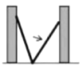
A.0.7米B.1.5米C.2.2米D.2.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线![]() :
:![]() 与
与![]() 轴相交于B,与
轴相交于B,与![]() 轴相交于点A.直线
轴相交于点A.直线![]() :
:![]() 经过原点,并且与直线
经过原点,并且与直线![]() 相交于C点.
相交于C点.
(1)求ΔOBC的面积;
(2)如图2,在![]() 轴上有一动点E,连接CE.问CE+
轴上有一动点E,连接CE.问CE+![]() BE是否有最小值,如果有,求出相应的点E的坐标及CE+
BE是否有最小值,如果有,求出相应的点E的坐标及CE+![]() BE的最小值;如果没有,请说明理由;
BE的最小值;如果没有,请说明理由;
(3)如图3,在(2)的条件下,以CE为一边作等边ΔCDE,D点正好落在![]() 轴上.将ΔDCE绕点D顺时针旋转,旋转角度为
轴上.将ΔDCE绕点D顺时针旋转,旋转角度为![]() (0°≤
(0°≤![]() ≤360),记旋转后的三角形为ΔDCE′,点C,E的对称点分别为C′,E′.在旋转过程中,设C′E′所在的直线与直线
≤360),记旋转后的三角形为ΔDCE′,点C,E的对称点分别为C′,E′.在旋转过程中,设C′E′所在的直线与直线![]() 相交于点M,与
相交于点M,与![]() 轴正半轴相交于点N.当ΔOMN为等腰三角形时,求线段ON的长?
轴正半轴相交于点N.当ΔOMN为等腰三角形时,求线段ON的长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m).
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com