
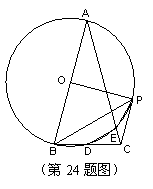
如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点![]() ,连结DE,过点B作BP平行于DE,交⊙O于点P,连结EP、CP、OP.
,连结DE,过点B作BP平行于DE,交⊙O于点P,连结EP、CP、OP.
(1)(3分)BD=DC吗?说明理由;
(2)(3分)求∠BOP的度数;
(3)(3分)求证:CP是⊙O的切线;
如果你解答这个问题有困难,可以参考如下信息:
为了解答这个问题,小明和小强做了认真的探究,然后分别用不同的思路完成了这个题目.在进行小组交流的时候,小明说:“设OP交AC于点G,证△AOG∽△CPG”;小强说:“过点C作CH⊥AB于点H,证四边形CHOP是矩形”.
1)BD=DC……………………………………1分
连结AD,∵AB是直径,∴∠ADB=90°……………………………………………2分
∵AB=AC,∴BD=DC……………………………………………………………3分
 (2)∵AD是等腰三角形ABC底边上的中线 ∴∠BAD=∠CAD ∴弧BD与弧DE是等弧,
(2)∵AD是等腰三角形ABC底边上的中线 ∴∠BAD=∠CAD ∴弧BD与弧DE是等弧,
∴BD=DE……………4分
∴BD=DE=DC,∴∠DEC=∠DCE ∵△ABC中,AB=AC,∠A=30°
∴∠DCE=∠ABC=![]() (180°-30°)=75°,∴∠DEC=75°
(180°-30°)=75°,∴∠DEC=75°
∴∠EDC=180°-75°-75°=30°
∵BP∥DE,∴∠PBC=∠EDC=30°……………………………5分
∴∠ABP=∠ABC-∠PBC=75°-30°=45°
∵OB=OP,∴∠OBP=∠OPB=45°,∴∠BOP=90° …………6分
(3)证法一:设OP交AC于点G,则∠AOG=∠BOP =90°
 在Rt△AOG中,∵∠OAG=30°,∴
在Rt△AOG中,∵∠OAG=30°,∴![]() ………………7分
………………7分
又∵![]() ,∴
,∴![]() ,∴
,∴![]()
又∵∠AGO=∠CGP
∴△AOG∽△CPG…………………………………8分
∴∠GPC=∠AOG=90°∴CP是⊙![]() 的切线………………………9分
的切线………………………9分
证法二:过点C作CH⊥AB于点H,则∠BOP=∠BHC=90°,∴PO∥CH
在Rt△AHC中,∵∠HAC=30°,∴![]() ………………7分
………………7分
又∵![]() ,∴PO=CH,∴四边形CHOP是平行四边形
,∴PO=CH,∴四边形CHOP是平行四边形
∴四边形CHOP是矩形……………………………8分
∴∠OPC=90°,∴CP是⊙![]() 的切线………………………9分
的切线………………………9分


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为A、
| ||||
B、(
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com