【题目】如图，
ABCD中，点
在边
上，以
为折痕，将
向上翻折，点
正好落在边
上的点
处，若
的周长为8，
的周长为18，则
的长为（ ）
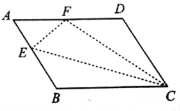
A.5B.8C.7D.6
字词句篇与同步作文达标系列答案科目：初中数学 来源： 题型：
【题目】某电子厂商投产一种新型电子产品，每件制造成本为18元，试销过程中发现，每月销售量y（万件）与销售单价x（元）之间的关系可以近似地看作一次函数
（利润=售价﹣制造成本）．
（1）写出每月的利润w（万元）与销售单价x（元）之间的函数关系式；
（2）当销售单价为多少元时，厂商每月能获得350万元的利润？
（3）当销售单价为多少元时，厂商每月能获得最大利润？最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(1)如图，用尺规作图的方法作出
的角平分线
. (保留作图痕迹，不要求写出作法)
(2)在(1)的基础上证明命题“全等三角形的对应角角平分线相等”是真命题.请填空并证明.
已知：如图，__________________，和
分别是
和
的平分线.
求证：______________________________.
证明：
查看答案和解析>>
科目：初中数学 来源： 题型：
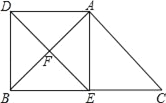
【题目】如图，E、F分别为△ABC的边BC、CA的中点，延长EF到D，使得DF=EF，连接DA、DB、AE．
（1）求证：四边形ACED是平行四边形；
（2）若AB=AC，试说明四边形AEBD是矩形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】足球运动员将足球沿与地面成一定角度的方向踢出，足球飞行的路线是一条抛物线，不考虑空气阻力，足球距离地面的高度
（单位：
）与足球被踢出后经过的时间
（单位：
）之间的关系如下表：
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论：①足球距离地面的最大高度为
；②足球飞行路线的对称轴是直线
；③足球被踢出
时落地；④足球被踢出
时，距离地面的高度是
.
其中正确结论的个数是（ ）
A．1 B．2 C．3 D．4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，矩形ABCD中，AE平分
交BC于E，
，则下面的结论：①
是等边三角形；②
；③
；④
，其中正确结论有（ ）
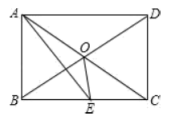
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长度为_____
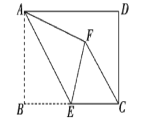
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“金源”食品加工厂需要一批食品包装盒，供应这种包装盒有两种方案可供选择：
方案一：从包装盒加工厂直接购买，购买所需的费用
（元）与包装盒个数
（个）满足图中的射线
所示的函数关系；
方案二：租赁机器自己加工，所需费用
（元）（包括租赁机器的费用和生产包装盒的费用）与包装盒个数（个）满足图中射线
所示的函数关系．
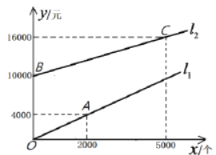
根据图象解答下列问题：
（1）点
的坐标是_____________，方案一中每个包装盒的价格是___________元，射线所表示的函数关系式是_____________．
（2）求出方案二中的与的函数关系式；
（3）你认为选择哪种方案更省钱？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，BE=CF，AB∥DE，添加下列哪个条件不能证明△ABC≌△DEF的是( )
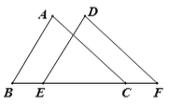
A. AB=DE B. ∠A=D C. AC=DF D. AC∥DF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
