
【题目】如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则cos∠OBC的值为( )
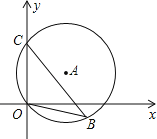
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
试题分析:连接CD,由∠COD为直角,根据90°的圆周角所对的弦为直径,可得出CD为圆A的直径,再利用同弧所对的圆周角相等得到∠CBO=∠CDO,在直角三角形OCD中,由CD及OC的长,利用勾股定理求出OD的长,然后利用余弦函数定义求出cos∠CDO的值,即为cos∠CBO的值.
解:连接CD,如图所示:
∵∠COD=90°,
∴CD为圆A的直径,即CD过圆心A,
又∵∠CBO与∠CDO为![]() 所对的圆周角,
所对的圆周角,
∴∠CBO=∠CDO,
又∵C(0,5),
∴OC=5,
在Rt△CDO中,CD=10,CO=5,
根据勾股定理得:OD=![]() =5
=5![]() ,
,
∴cos∠CBO=cos∠CDO=![]() =
=![]() =
=![]() .
.
故选B



科目:初中数学 来源: 题型:
【题目】根据下列已知条件,能惟一画出△ABC的是( )
A. AB=3,BC=4,CA=8 B. ∠A=60°,∠B=45°,AB=4
C. AB=4,BC=3,∠A=30° D. ∠C=90°,AB=6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句中,真命题有( )个
①在同一平面内,过一点有且只有一条直线与已知直线平行;
②相等的角是对顶角;
③若两个角有公共顶点且有一条公共边,和等于平角,则这两个角为邻补角;
④平方根和立方根相等的数是0;
⑤平移变换中,各组对应点连成的线段平行且相等.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有黄色、白色乒乓球共40个,除颜色外其他完全相同.小明从这个袋子中随机摸出一球,放回.通过多次摸球实验后发现,摸到黄色球的概率稳定在15%附近,则袋中黄色球可能有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
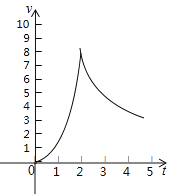
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.
(3)求弹珠离开轨道时的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )
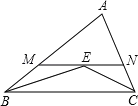
A.6 B.7 C.8 D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=![]() (k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.

(1)求点A的坐标及一次函数解析式.
(2)求点C的坐标及反比例函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com