
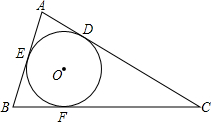
 如图,已知⊙O为△ABC的内切圆,D、E、F为切点,P是异于E、F的⊙O上一动点,若∠A+∠C=130°,则∠EPF等于65°或115°.
如图,已知⊙O为△ABC的内切圆,D、E、F为切点,P是异于E、F的⊙O上一动点,若∠A+∠C=130°,则∠EPF等于65°或115°. 分析 有两种情况:①当P在优弧EDF上时,连接OE、OF,求出∠EOF,根据圆周角定理求出即可;②当P在劣弧EMF上时,根据圆内接四边形的性质得到∠EPF+∠EDF=180°,代入求出即可.
解答 解:连接OE、OF、ED、FD,
∵⊙O为△ABC的内切圆,D、E、F为切点,
∴∠BEO=∠BFO=90°,
∵∠A+∠C=130°,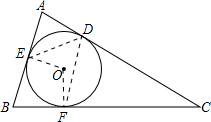
∴∠B=50°,
∴∠EOF=130°,∠EDF=$\frac{1}{2}$∠EOF=65°,
有两种情况:
①当P在优弧EDF上时,∠EPF=∠EDF=65°,
②当P在劣弧EMF上时,∠EPF+∠EDF=180°,
∠FPE=180°-65°=115°.
故答案为:65°或115°.
点评 本题主要考查了多边形的内角和定理,三角形的内切圆与内心,圆周角定理等知识点的理解和掌握,能综合运用性质进行推理是解此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | -$\frac{7}{2}$或$\frac{1}{2}$ | D. | 2或-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
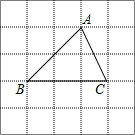 如图所示的方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),在图中画出与△ABC有一条公共边BC且全等的所有格点三角形.
如图所示的方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),在图中画出与△ABC有一条公共边BC且全等的所有格点三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 关于x轴对称 | B. | 关于y轴对称 | ||
| C. | 关于直线y=x轴对称 | D. | 关于直线y=-x对称 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com