
【题目】小图暑假期间参加社会实践活动,从某批发市场以每个a元的价格购进50个手机充电宝,然后每个加价b元到市场出售.
(1)求全部售出50个手机充电宝的总销售额为多少元(结果用含a,b的式子表示)?
(2)由于开学临近,小丽在成功售出30个充电宝后,决定将剩余充电宝按售价8折出售,并很快全部售完.
①她的总销售额是多少元?
②相比不采取降价销售,她将比实际销售多盈利多少元(结果用含a、b的式子表示)
③若a=2b,小丽实际销售完这批充电宝的利润率为 (利润率=利润÷进价100%).
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
【题目】某市区自2014年1月起,居民生活用水开始实行阶梯式计量水价,该阶梯式计量水价分为三级(如下表所示):
月用水量(吨) | 水价(元/吨) |
第一级 20吨以下(含20吨) | 1.6 |
第二级 20吨﹣30吨(含30吨) | 2.4 |
第三级 30吨以上 | 3.2 |
(1)如果甲用户的月用水量为12吨,则甲需缴的水费为 元;
(2)如果乙用户缴的水费为39.2元,则乙月用水量 吨;
(3)如果丙用户的月用水量为![]() 吨,则丙用户该月应缴水费多少元?(用含a的代数式表示,并化简)
吨,则丙用户该月应缴水费多少元?(用含a的代数式表示,并化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销量y(件)之间的关系如下表:若日销量y是销售价x的一次函数.
(1)求出日销量y(件)与销售价x(元)的函数关系式;
(2)求销售定价为30元时,每日的销售利润.
x(元) | 15 | 20 | 25 | …… |
y(件) | 25 | 20 | 15 | …… |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
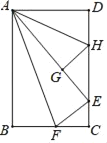
【题目】在数学拓展课《折叠矩形纸片》上,小林折叠矩形纸片ABCD进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕AF交BC边于点F;②把△ADH翻折,点D落在AE边长的点G处,折痕AH交CD边于点H.若AD=6,AB=10,则![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,过抛物线![]() 与y轴的交点作y轴的垂线,则称这条垂线是该抛物线的伴随直线.例如:抛物线
与y轴的交点作y轴的垂线,则称这条垂线是该抛物线的伴随直线.例如:抛物线![]() 的伴随直线为直线
的伴随直线为直线![]() .抛物线
.抛物线![]() 的伴随直线l与该抛物线交于点A、D(点A在y轴上),该抛物线与x轴的交点为B(-1,0)和C(点C在点B的右侧).
的伴随直线l与该抛物线交于点A、D(点A在y轴上),该抛物线与x轴的交点为B(-1,0)和C(点C在点B的右侧).
(1)若直线l是y=2,求该抛物线对应的函数关系式.
(2)求点D的坐标(用含m的代数式表示).
(3)设抛物线![]() 的顶点为M,作OA的垂直平分线EF,交OA于点E,交该抛物线的对称轴于点F.
的顶点为M,作OA的垂直平分线EF,交OA于点E,交该抛物线的对称轴于点F.
①当△ADF是等腰直角三角形时,求点M的坐标.
②将直线EF沿直线l翻折得到直线GH,当点M到直线GH的距离等于点C到直线EF的距离时,直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,我们可以用大写英文字母表示一条线段的两个端点,比如A,B;那么这条线段可以记为线段AB(或线段BA).若线段AB的长等于5,我们表示线段AB=5.若点P把线段MN分成相等的两条线段MP与PN,则称点P为线段MN的中点.根据上述材料,解答下列问题:
已知数轴上,点O为原点,点A表示的数为8,动点B,C在数轴上移动,且总保持BC=2(点C在点B右侧),设点B表示的数为m.
![]()
![]()
(1)如图1,当B,C在线段OA上移动时,
① 若B为OA中点,则AC= ;
② 若B,C移动到某一位置时,恰好满足AC=OB,求此时m的值;
(2)当线段BC在数轴上移动时,请结合数轴代数式![]() 的值是否存在最小值?若存在,请直接写出其最小值和此时m所满足的条件;若不存在,请说明理由.
的值是否存在最小值?若存在,请直接写出其最小值和此时m所满足的条件;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com