
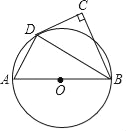
【题目】如图,AB为⊙O的直径,点C在⊙O外,∠ABC的平分线与⊙O交于点D,∠C=90°.
(1)CD与⊙O有怎样的位置关系?请说明理由;
(2)若∠CDB=60°,AB=6,求![]() 的长.
的长.

【答案】(1)相切,理由见解析;(2)π.
【解析】
(1)连接OD,根据BD是∠ABC的平分线的性质有∠CBD=∠ABD,根据OD=OB,得到∠ODB=∠ABD,等量代换得到∠ODB=∠CBD,根据平行线的判定得到OD∥CB,根据平行线的性质有∠ODC=∠C=90°,即可证明CD与⊙O相切;
(2)根据扇形的弧长公式进行计算即可.
(1)相切.理由如下:
连接OD,
∵BD是∠ABC的平分线,
∴∠CBD=∠ABD,
又∵OD=OB,
∴∠ODB=∠ABD,
∴∠ODB=∠CBD,
∴OD∥CB,
∴∠ODC=∠C=90°,
∴CD与⊙O相切;
(2)若∠CDB=60°,可得∠ODB=30°,
∴∠AOD=60°,
又∵AB=6,
∴AO=3,
∴![]()
![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(Ⅰ)若设AP=x,则PC= ,QC= ;(用含x的代数式表示)
(Ⅱ)当∠BQD=30°时,求AP的长;
(Ⅲ)在运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级全体同学参加了“爱心一日捐捐款活动,该校随杋抽査了部分同学捐款的情况统计如图所示:

(1)求出本次抽查的学生人数;
(2)求出捐款10元的学生人数,并将条形图补充完整;
(3)捐款金额的众数是 元,中位数是 .
(4)请估计全校八年级1000名学生,捐款20元的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,先描出点![]() ,点
,点![]() .
.

(1)描出点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 的位置,写出
的位置,写出![]() 的坐标 ;
的坐标 ;
(2)用尺规在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小(保留作图痕迹);
的值最小(保留作图痕迹);
(3)用尺规在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() (保留作图痕迹).
(保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线, DE⊥AB于点E.

(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,且MB=MG.试探究ND,DG与AD数量之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 和
和![]() 都是等边三角形,点
都是等边三角形,点![]() 、
、![]() 、
、![]() 在同一条直线上,
在同一条直线上,![]() 、
、![]() 分别与
分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,
,![]() 和
和![]() 交于点
交于点![]() ,有如下结论:①
,有如下结论:①![]() 是等边三角形;②
是等边三角形;②![]() ;③
;③![]() ≌
≌![]() ;④
;④![]() ;⑤
;⑤![]() 平分
平分![]() ;⑥
;⑥![]() ;⑦
;⑦![]() .其中不正确的结论的个数是( )
.其中不正确的结论的个数是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com