练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

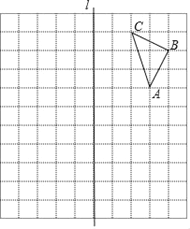
    【题目】如图，直线l与△ABC在边长为1个单位长度的小正方形网格中，点A，B，C都为网格线的交点．

    （1）请画出△ABC关于直线l对称的△A1B1C1（点A，B，C的对称点分别为A1，B1，C1）.

    （2）请画出将线段AC向左平移3个单位，再向下平移5个单位得到的线段A2C2（点A，C的对应点分别为A2，C2），再以A2C2为斜边画一个等腰直角三角形A2B2C2．

    【答案】（1）见解析；（2）见解析.

    【解析】

    （1）根据轴对称的定义作出对应点，再顺次连接可得；

    （2）先根据平移的定义作出平移后的对应点，再连接可得线段，根据等腰直角三角形的定义结合网格可得答案．

    （1）如图所示，△A1B1C1即为所求；

    （2）如图所示，A2C2和△A2B2C2或△A2B′2C2即为所求．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图是某月的日历表，在此目历表上可以用一个“十”字圈出5个数．

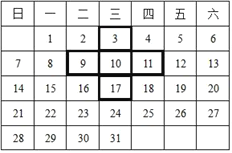
    (1)如图中四周的4个数3、9、17、11的和与中间的数10有什么数量关系？

    (2)照此方法，任意圈出的5个数是否都具有这样的数量关系？请通过整式的运算说明理由．

    (3)用(2)的结论说明圈出的5个数的和能否等于125？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°，此时该同学距地面高度AE为20米，电梯再上升5米到达D点，此时测得大楼BC楼顶B点的仰角为37°，求大楼的高度BC．
    （参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）．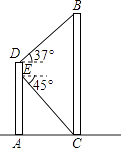

    查看答案和解析>>

    科目：初中数学 来源： 题型：

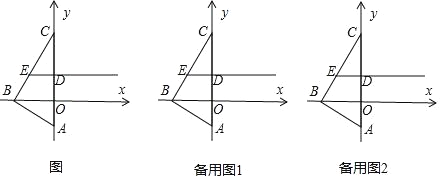
    【题目】如图，在平面直角坐标系中，△ABC的顶点A的坐标为（0，﹣1），顶点B在x轴的负半轴上，顶点C在y轴的正半轴上，且∠ABC＝90°，∠ACB＝30°，线段OC的垂直平分线分别交OC，BC于点D，E．

    （1）点C的坐标；

    （2）点P为线段ED的延长线上的一点，连接PC，PA，设点P的横坐标为t，△ACP的面积为S，求S与t的函数关系式；

    （3）在（2）的条件下，点F为线段BC的延长线上一点，连接OF，若OF＝CP，求∠OFP的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，填空:

    (1)若∠4=∠3，则____∥_____，理由是______；

    (2)若∠2=∠E，则____∥___，理由是____；

    (3)若∠A=∠ABE=180°，则____∥___，理由是____；

    (4)若∠2=∠____，则DA∥EB，理由是____；

    (5)若∠DBC+∠_____=180°，则DB∥EC，理由是____；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，在三角形ABC中，点E，F分别为线段AB，AC上任意两点，EG交BC于点G，交AC的延长线于点H，∠1＋∠AFE＝180°.

    (1)证明：BC∥EF；

    (2)如图②，若∠2＝∠3，∠BEG＝∠EDF，证明：DF平分∠AFE.

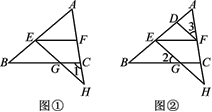
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，反比例函数y= （x＞0）的图象经过矩形OABC对角线的交点M，分别与AB、BC相交于点D、E．，则下列结论正确的是（将正确的结论填在横线上）．
    ①s△OEB=s△ODB ， ②BD=4AD，③连接MD，S△ODM=2S△OCE ， ④连接ED，则△BED∽△BCA．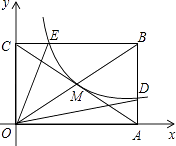

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，C为∠AOB的边OA上一点，OC=6，N为边OB上异于点O的一动点，P是线段CN上一点，过点P分别作PQ∥OA交OB于点Q，PM∥OB交OA于点M．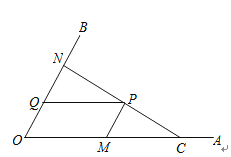

    （1）若∠AOB=60°，OM=4，OQ=1，求证：CN⊥OB
    （2）当点N在边OB上运动时，四边形OMPQ始终保持为菱形．
    ①问：﹣的值是否发生变化？如果变化，求出其取值范围；如果不变，请说明理由．
    ②设菱形OMPQ的面积为S1 ， △NOC的面积为S2 ， 求的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】完成下面的推理．

    如图，BE平分∠ABD，DE平分∠BDC，且∠α＋∠β＝90°，试说明：AB∥CD.

    完成推理过程：

    ∵BE平分∠ABD(已知)，

    ∴∠ABD＝2∠α(__________)．

    ∵DE平分∠BDC(已知)，

    ∴∠BDC＝2∠β (__________)．

    ∴∠ABD＋∠BDC＝2∠α＋2∠β＝2(∠α＋∠β)( __________)．

    ∵∠α＋∠β＝90°(已知)，

    ∴∠ABD＋∠BDC＝180°(__________)．

    ∴AB∥CD(____________________)．

    查看答案和解析>>

    同步练习册答案