
【题目】小赵投资销售一种进价为每件20元的护眼台灯.销售过程中发现,当月内销售单价不变,则月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:![]() .
.
(1)设小赵每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?并求出最大利润.
(2)如果小赵想要每月获得的利润不低于2000元,那么如何制定销售单价才可以实现这一目标?
【答案】(1)当销售单价定为35元时,每月获得的利润最大,最大利润为2250元;
(2)如果小赵想要每月获得的利润不低于2000元,那么他的销售单价应不低于30元而不高于40元.
【解析】
试题(1)根据总利润=单利润×销售量即可得到函数关系式,再根据二次函数的性质即得结果;
(2)先求得利润为2000元时对应的销售单价,再根据二次函数的性质即可求得结果.
(1)由题意得w=(x-20)·y=(x-20)·(![]() )
)![]()
当![]() 时,
时,![]() ;
;
(2)由题意得![]()
解得x1 =30,x2 =40
即小赵想要每月获得2000元的利润,销售单价应定为30元或40元
∵![]()
∴抛物线开口向下
∴当30≤x≤40时,w≥2000
答:(1)当销售单价定为35元时,每月可获得最大利润,且最大利润为2250元;
(2)如果小赵想要每月获得的利润不低于2000元,那么他的销售单价应不低于30元而不高于40元.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.过点C作CD∥x轴,交抛物线的对称轴于点D.
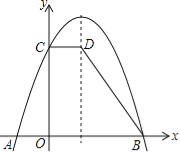
(1)求该抛物线的解析式;
(2)若将该抛物线向下平移m个单位,使其顶点落在D点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆.
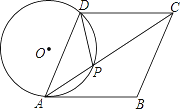
(1)求证:AB是⊙O的切线;
(2)若AC=8,tan∠BAC=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
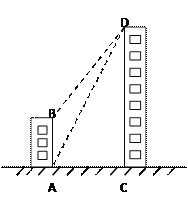
【题目】如图,一栋居民楼AB的高为16米,远处有一栋商务楼CD,小明在居民楼的楼底A处测得商务楼顶D处的仰角为![]() ,又在商务楼的楼顶D处测得居民楼的楼顶B处的俯角为
,又在商务楼的楼顶D处测得居民楼的楼顶B处的俯角为![]() .其中A、C两点分别位于B、D两点的正下方,且A、C两点在同一水平线上,求商务楼CD的高度.
.其中A、C两点分别位于B、D两点的正下方,且A、C两点在同一水平线上,求商务楼CD的高度.
(参考数据: ![]() ,
, ![]() .结果精确到0.1米)
.结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
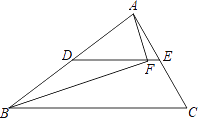
【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
A.如图,DE为△ABC的中位线,点F为DE上一点,且∠AFB=90°,若AB=8,BC=10,则EF的长为________.
B.小智同学在距大雁塔塔底水平距离为138米处,看塔顶的仰角为24.8(不考虑身高因素),则大雁塔市约为________米.(结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM=![]() AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是
AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是![]() ,则
,则![]() 的值是 .
的值是 .
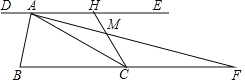
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并解决相应问题:
材料一:换元法是数学中的重要方法,利用换元法可以从形式上简化式子,在求解某些特殊方程时,利用换元法常常可以达到转化的目的,例如在求解一元四次方程![]() ,就可以令
,就可以令![]() ,则原方程就被换元成
,则原方程就被换元成![]() ,解得 t 1,即
,解得 t 1,即![]() ,从而得到原方程的解是 x 1
,从而得到原方程的解是 x 1
材料二:杨辉三角形是中国数学上一个伟大成就,在中国南宋数学家杨辉 1261 年所著的《详解九章算法》一书中出现,它呈现了某些特定系数在三角形中的一种有规律的几何排列,下图为杨辉三角形:

……………………………………
(1)利用换元法解方程:![]()
(2)在杨辉三角形中,按照自上而下、从左往右的顺序观察, an 表示第 n 行第 2 个数(其中 n≥4),bn 表示第 n 行第 3 个数,![]() 表示第
表示第![]() 行第 3 个数,请用换元法因式分解:
行第 3 个数,请用换元法因式分解:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ABC=90°,AB=BC,E、M分别为AB、AC上的点,连接CE,BM交于点G,且BM⊥CE,O为AC的中点,连接BO交CE于点N.
(1)如图①,若AB=6,2MO=AM,求BM的长;
(2)如图②,连接OG、AG,若AG⊥OG,求证:AC=![]() BG.
BG.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com