
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足 ![]() =
= ![]() ,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE=
,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE= ![]() ;④S△DEF=4
;④S△DEF=4 ![]() ,其中正确的是( )
,其中正确的是( ) 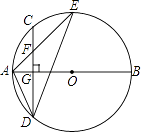
A.①②③
B.②③④
C.①②④
D.①③④
【答案】C
【解析】解:①∵AB是⊙O的直径,弦CD⊥AB, ∴ ![]() ,DG=CG,
,DG=CG,
∴∠ADF=∠AED,
∵∠FAD=∠DAE(公共角),
∴△ADF∽△AED;
故①正确;
②∵ ![]() =
= ![]() ,CF=2,
,CF=2,
∴FD=6,
∴CD=DF+CF=8,
∴CG=DG=4,
∴FG=CG﹣CF=2;
故②正确;
③∵AF=3,FG=2,
∴AG= ![]() =
= ![]() ,
,
∴在Rt△AGD中,tan∠ADG= ![]() =
= ![]() ,
,
∴tan∠E= ![]() ;
;
故③错误;
④∵DF=DG+FG=6,AD= ![]() =
= ![]() ,
,
∴S△ADF= ![]() DFAG=
DFAG= ![]() ×6×
×6× ![]() =3
=3 ![]() ,
,
∵△ADF∽△AED,
∴ ![]() =(
=( ![]() )2 ,
)2 ,
∴ ![]() =
= ![]() ,
,
∴S△AED=7 ![]() ,
,
∴S△DEF=S△AED﹣S△ADF=4 ![]() ;
;
故④正确.
故选C.
①正确.由AB是⊙O的直径,弦CD⊥AB,根据垂径定理可得: ![]() ,DG=CG,继而证得△ADF∽△AED;
,DG=CG,继而证得△ADF∽△AED;
②正确.由 ![]() =
= ![]() ,CF=2,可求得DF的长,继而求得CG=DG=4,则可求得FG=2;
,CF=2,可求得DF的长,继而求得CG=DG=4,则可求得FG=2;
③错误.由勾股定理可求得AG的长,即可求得tan∠ADF的值,继而求得tan∠E= ![]() .
.
④首先求得△ADF的面积,由相似三角形面积的比等于相似比的平方,即可求得△ADE的面积,继而求得S△DEF=4 ![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,MN是⊙O的直径,MN=4,∠AMN=30°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( ) 
A.2
B.2 ![]()
C.4 ![]()
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入相应的集合中:
-6, 9.3, -![]() , 15, 0, -0.33, -0.333…, 1.41421356, -3
, 15, 0, -0.33, -0.333…, 1.41421356, -3![]() , 3.3030030003…, -3.1415926.
, 3.3030030003…, -3.1415926.
正数集合:{ … }
负数集合: { … }
有理数集合: { … }
无理数集合: { … }
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明有5张写着不同数的卡片,请你按照题目要求抽出卡片,完成下列问题:
(1)从中取出3张卡片,使这3张卡片上数字的乘积最大,如何抽取?最大值是多少?
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,如何抽取?最小值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
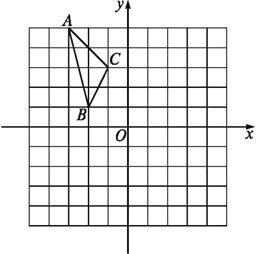
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)画出△ABC经过平移后得到的△A1B1C1,已知点C1的坐标为(4,0),并写出顶点B1的坐标;
(2)若△ABC和△A2B2C2关于原点O成中心对称,画出△A2B2C2 ,写出顶点B2的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,,画出图形并写出△A3B3C3顶点B3的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
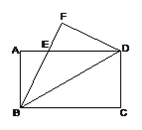
【题目】如图把长方形沿对角线折叠,重合部分为△EBD。
(1) △EBD是等腰三角形吗?为什么?
(2) 若AB=12cm,BC=18cm,求AE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成长方形零件PQMN,使长方形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上,求这个长方形零件PQMN面积S的最大值. 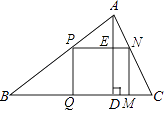
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平整的地面上,用若干个棱长完全相同的小正方体堆成一个几何体.
(1)请画出这个几何体的三视图.
(2)如果现在你手头还有一些相同的小正方体,要求保持俯视图和左视图不变,最多可以再添加几个小正方体


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com