
【题目】如图,平面直角坐标系中,一次函数y=x﹣1的图象与x轴,y轴分别交于点A,B,与反比例函数y=![]() 的图象交于点C,D,CE⊥x轴于点E,
的图象交于点C,D,CE⊥x轴于点E,![]() .
.
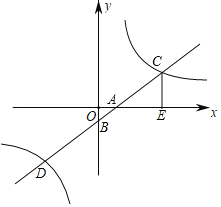
(1)求反比例函数的表达式与点D的坐标;
(2)以CE为边作ECMN,点M在一次函数y=x﹣1的图象上,设点M的横坐标为a,当边MN与反比例函数y=![]() 的图象有公共点时,求a的取值范围.
的图象有公共点时,求a的取值范围.
【答案】(1)D(﹣3,﹣4);(2)当边MN与反比例函数y=![]() 的图象有公共点时4<a≤6或﹣3<a≤﹣2.
的图象有公共点时4<a≤6或﹣3<a≤﹣2.
【解析】
(1)利用待定系数法以及等腰直角三角形的性质求出EC,OE即可解决问题.
(2)如图,设M(a,a﹣1),则N(a,![]() ),由EC=MN构建方程求出特殊点M的坐标即可判断.
),由EC=MN构建方程求出特殊点M的坐标即可判断.
解:(1)由题意A(1,0),B(0,﹣1),
∴OA=OB=1,
∴∠OAB=∠CAE=45°
∵AE=3OA,
∴AE=3,
∵EC⊥x轴,
∴∠AEC=90°,
∴∠EAC=∠ACE=45°,
∴EC=AE=3,
∴C(4,3),
∵反比例函数y=![]() 经过点C(4,3),
经过点C(4,3),
∴k=12,
由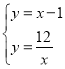 ,解得
,解得![]() 或
或![]() ,
,
∴D(﹣3,﹣4).
(2)如图,设M(a,a﹣1),则N(a,![]() )
)
∵四边形ECMN是平行四边形,
∴MN=EC=3,
∴|a﹣1﹣![]() |=3,
|=3,
解得a=6或﹣2或﹣1±![]() (舍弃),
(舍弃),
∴M(6,5)或(﹣2,﹣3),
观察图象可知:当边MN与反比例函数y=![]() 的图象有公共点时4<a≤6或﹣3<a≤﹣2.
的图象有公共点时4<a≤6或﹣3<a≤﹣2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,四边形OABC的顶点A在![]() 轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点.
轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点.
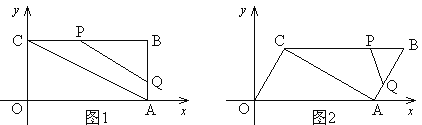
(1)若四边形OABC为矩形,如图1,
①求点B的坐标;
②若BQ:BP=1:2,且点B1落在OA上,求点B1的坐标;
(2)若四边形OABC为平行四边形,如图2,且OC⊥AC,过点B1作B1F∥![]() 轴,与对角线AC、边OC分别交于点E、点F.若B1E: B1F=1:3,点B1的横坐标为
轴,与对角线AC、边OC分别交于点E、点F.若B1E: B1F=1:3,点B1的横坐标为![]() ,求点B1的纵坐标,并直接写出
,求点B1的纵坐标,并直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
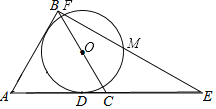
【题目】如图,△ABC为等边三角形,O为BC的中点,作⊙O与AC相切于点D.
(1)求证:AB与⊙O相切;
(2)延长AC到E,使得CE=AC,连接BE交⊙O与点F、M,若AB=4,求FM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数都表示为两个素数的和”.如20=3+17.
(1)从7、11、19、23这4个素数中随机抽取一个,则抽到的数是7的概率是 ;
(2)从7、11、19、23这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,用画树状图或列表的方法,求抽到的两个素数之和等于30的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读,我们可以用换元法解简单的高次方程,解方程x4﹣3x2+2=0时,可设y=x2,则原方程可比为y2+3y+2=0,解之得y1=2,y2=1,当y1=2时,则x2=2,即x1=![]() ,x2=﹣
,x2=﹣![]() ;当y2=1时,即x2=1,则x1=1,x2=﹣1,故原方程的解为x1=
;当y2=1时,即x2=1,则x1=1,x2=﹣1,故原方程的解为x1=![]() ,x2=﹣
,x2=﹣![]() ,x3=1,x4=﹣1,仿照上面完成下面解答:
,x3=1,x4=﹣1,仿照上面完成下面解答:
(1)已知方程(2x2+1)2+2x2﹣3=0,设y=2x2+1,则原方程可化为_______.
(2)仿照上述解法解方程:(x2﹣2x)2﹣3x2+6x=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,某景区商店推出销售纪念品活动,已知纪念品每件的进货价为30元,经市场调研发现,当该纪念品的销售单价为40元时,每天可销售280件;当销售单价每增加1元,每天的销售数量将减少10件.(销售利润=销售总额﹣进货成本)
(1)若该纪念品的销售单价为45元时,则当天销售量为 件.
(2)当该纪念品的销售单价为多少元时,该纪念品的当天销售利润是2610元.
(3)当该纪念品的销售单价定为多少元时,该纪念品的当天销售利润达到最大值?求此最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com