
【题目】![]() 如图
如图![]() ,在正方形
,在正方形![]() 中,点
中,点![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,垂足为
,垂足为![]() ,那么
,那么![]() 与
与![]() ________(“相等”或“不相等”)26.
________(“相等”或“不相等”)26.
![]() 如图
如图![]() ,将边长为
,将边长为![]() 的正方形纸片
的正方形纸片![]() 沿
沿![]() 折叠,使得点
折叠,使得点![]() 落到边
落到边![]() 上.若
上.若![]() ,求出
,求出![]() 和
和![]() 的长度.
的长度.

【答案】(1)相等;(2)![]()
【解析】
(1)可过点E作EH∥AD,证明Rt△ABG≌Rt△EHF即可得出结论.
(2)借助对称原理,根据勾股定理即可求出BE、AG的长;利用第(1)问中的结论即可获得EF的长.
(1)如图(1)所示,

过点E作EH∥AD,交CD于H;则四边形AEHD为矩形;
∴EH=AD=AB;
∵AG⊥EF,EH∥AD,
∴∠BAG+∠AEF=90°,∠AEF+∠FEH=90°,
∴∠BAG=∠FEH;在△ABG与△EHF中,
∵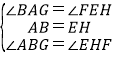 ,
,
∴△ABG≌△EHF(ASA)
∴AG=EF.
故答案为相等;
![]() 如图
如图![]() ,连接
,连接![]() ;
;

设![]() ,则
,则![]() ;由对称原理得:
;由对称原理得:![]() ,
,![]() ,
,
∴![]() ;由问题
;由问题![]() 知:
知:![]() ;
;
∵四边形![]() 为正方形,
为正方形,
∴![]() ;
;
由勾股定理得:![]() ,
,![]() ;
;
![]() ,解得
,解得![]() ,
,
∴![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)如图1,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
①画出△ABC关于x轴的对称图形△A1B1C1;
②画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2;
③如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是 .
(2)请在图2用无刻度的直尺在图中以AB为一边画一个面积为18的长方形ABMN.(不要求写画法,但要保留画图痕迹)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为( ).

A.126°B.110°C.108°D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为![]() 的菱形
的菱形![]() 中,
中,![]() ,以对角线
,以对角线![]() 为边作第
为边作第![]() 个菱形
个菱形![]() ,使
,使![]() .连结
.连结![]() ,再以
,再以![]() 为边作第
为边作第![]() 个菱形
个菱形![]() 使
使![]() …,则第
…,则第![]() 个菱形的边长是________,按此规律所作第
个菱形的边长是________,按此规律所作第![]() 个菱形的边长是________.
个菱形的边长是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=50°,∠ACB=80°,延长CB至D,使DB=BA,延长BC至E,使CE=CA,连接AD,AE.求∠D,∠E,∠DAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DH⊥AC于点H.
(1)判断DH与⊙O的位置关系,并说明理由;
(2)求证:H为CE的中点;
(3)若BC=10,cosC=![]() ,求AE的长.
,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店销售一种品牌的羽绒服,平均每天可以销售![]() 件,每件盈利
件,每件盈利![]() 元,为了扩大销售,减少库存,商店决定降价销售,经调查,每件羽绒服每降价
元,为了扩大销售,减少库存,商店决定降价销售,经调查,每件羽绒服每降价![]() 元时,平均每天就多卖出
元时,平均每天就多卖出![]() 件,但是综合多方因素,降价后,每件盈利不能低于原来每件利润的一半.
件,但是综合多方因素,降价后,每件盈利不能低于原来每件利润的一半.
![]() 若商场要求该羽绒服每天盈利
若商场要求该羽绒服每天盈利![]() 元,每件羽绒服应降价多少元?
元,每件羽绒服应降价多少元?
![]() 试说明每件羽绒服降价多少元时,盈利最多?
试说明每件羽绒服降价多少元时,盈利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:

(1)∠BAE的度数;
(2)∠DAE的度数;
(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B-∠C=40°,也能得出∠DAE的度数?若能,请你写出求解过程;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com