
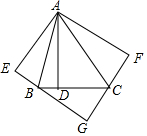
 如图,在△ABC中,∠BAC=45°,AD⊥BC于点D,$\frac{BD}{DC}$=$\frac{2}{3}$,AD=6,将△ADB,△ADC分别沿AB,AC翻折得△ABE,△ACF,延长EB,FC相交于点G.
如图,在△ABC中,∠BAC=45°,AD⊥BC于点D,$\frac{BD}{DC}$=$\frac{2}{3}$,AD=6,将△ADB,△ADC分别沿AB,AC翻折得△ABE,△ACF,延长EB,FC相交于点G.分析 (1)由折叠的性质得出AE=AD=AF,BE=BD,CF=CD,∠E=∠F=90°,∠BAE=∠BAD,∠CAF=∠CAD,证出∠EAF=90°,判定四边形AEGF是矩形,即可得出结论;
(2)由正方形的性质得出∠G=90°,GE=GF=AE=AD=6,设BD=2x,CD=3x,则BE=BD=2x,CF=CD=3x,BG=6-2x,CG=6-3x,在Rt△BCG中,由勾股定理得出方程,解方程求出BC的长,再由三角形面积公式即可得出答案.
解答 (1)证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°;
由折叠可知,AE=AD=AF,BE=BD,CF=CD,∠E=∠F=90°,∠BAE=∠BAD,∠CAF=∠CAD,
∴∠BAE+∠CAF=∠BAD+∠CAD=∠BAC=45°;
∴∠EAF=∠BAE+∠CAF+∠BAC=90°;
∴四边形AEGF是矩形,
又∵AE=AF,
∴四边形AEGF是正方形;
(2)解:∵四边形AEGF是正方形,
∴∠G=90°,GE=GF=AE=AD=6,
∵$\frac{BD}{DC}$=$\frac{2}{3}$,
∴设BD=2x,CD=3x,
则BE=BD=2x,CF=CD=3x,BG=6-2x,CG=6-3x,
在Rt△BCG中,BG2+CG2=BC2,
∴(6-2x)2+(6-3x)2=(5x)2,
解得x1=1,x2=-6(不合题意,舍去),
∴BC=5,
∴△ABC的面积=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×5×6=15,
点评 此题主要考查了折叠的性质、勾股定理、正方形的判定和性质等知识;熟练掌握折叠的性质和勾股定理是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | -1 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
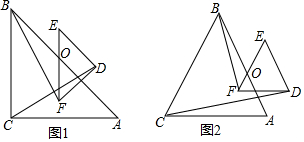
 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,点A在y轴上,点O,B1,B2,B3…都在直线l上,则点B2017的坐标是(2017$\sqrt{3}$,2017).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,点A在y轴上,点O,B1,B2,B3…都在直线l上,则点B2017的坐标是(2017$\sqrt{3}$,2017).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
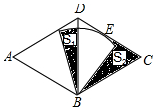 如图,菱形ABCD,∠A=60°,AB=4,以点B为圆心的扇形与边CD相切于点E,扇形的圆心角为60°,点E是CD的中点,图中两块阴影部分的面积分别为S1,S2,则S2-S1=2$\sqrt{3}$-π.
如图,菱形ABCD,∠A=60°,AB=4,以点B为圆心的扇形与边CD相切于点E,扇形的圆心角为60°,点E是CD的中点,图中两块阴影部分的面积分别为S1,S2,则S2-S1=2$\sqrt{3}$-π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
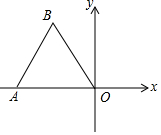 如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为2的等边三角形.
如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为2的等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若$\frac{x}{a}$<$\frac{y}{a}$,则x<y | B. | 若bx>by,则x>y | C. | 若$\frac{x}{a}$=$\frac{y}{a}$,则x=y | D. | 若mx=my,则x=y |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
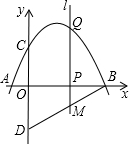 如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),B(4,0),与y轴交于点C(0,2),点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l,交抛物线于点Q.
如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),B(4,0),与y轴交于点C(0,2),点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l,交抛物线于点Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com