
 如图,△ABC中,∠ACB=90°,BC=4,AC=8,△FDE≌△ABC.△FDE顶点D与边AB的中点重合,DE,DF分别交AC于点P,Q,若重叠部分△DPQ是以DP为一腰的等腰三角形,则它的面积为$\frac{5}{2}$或2$\sqrt{5}$-2.
如图,△ABC中,∠ACB=90°,BC=4,AC=8,△FDE≌△ABC.△FDE顶点D与边AB的中点重合,DE,DF分别交AC于点P,Q,若重叠部分△DPQ是以DP为一腰的等腰三角形,则它的面积为$\frac{5}{2}$或2$\sqrt{5}$-2. 分析 分两种情况:
①当PD=PQ时,如图1所示:
过点D作DK⊥AC于点K,则DK∥BC,作辅助线,利用相似三角形、勾股定理、等腰三角形的性质,列方程求解;
②当PD=DQ时,如图2,用辅助线,利用等腰三角形三线合一的性质和平行线的性质得:∠FDM=∠EDM,∠NMD=∠EDM,设MN=DN=x,利用同角的三角函数表示FN=4$\sqrt{5}$-x,由勾股定理列方程求出x的值,从而求得S△PDQ的值.
解答 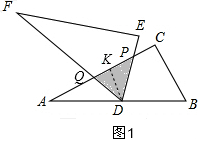 解:分两种情况:
解:分两种情况:
①当PD=PQ时,如图1所示:
过点D作DK⊥AC于点K,则DK∥BC,
又∵点D为AB中点,
∴DK=$\frac{1}{2}$BC=$\frac{1}{2}×4$=2,
∵PD=PQ,
∴∠PQD=∠PDQ,由∠PDQ=∠B,
∴∠PQD=∠B,
又∵∠DKQ=∠C=90°,
∴△DKQ∽△ACB,
∴$\frac{KQ}{BC}=\frac{DK}{AC}$,即$\frac{KQ}{4}=\frac{2}{8}$,得KQ=1,
设PD=PQ=x,则PK=x-1,
在Rt△DMK中,由勾股定理得:PK2+DK2=PD2,
即:(x-1)2+22=x2,解得x=$\frac{5}{2}$,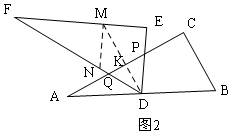
∴S△PDQ=$\frac{1}{2}$PQ•DK=$\frac{1}{2}$×$\frac{5}{2}$×2=$\frac{5}{2}$.
②当PD=DQ时,如图2所示,
过D作DK⊥AC,交AC于K,交EF于M,过M作MN⊥EF,交DF于N,则MN∥DE,
∴∠FDM=∠EDM,∠NMD=∠EDM,
∴∠FDM=∠NMD,
∴MN=DN,
设MN=DN=x,
tan∠F=$\frac{DE}{EF}=\frac{MN}{FM}$=$\frac{4}{8}=\frac{1}{2}$,
∴FM=2x,
∵FD=AB=4$\sqrt{5}$,
∴FN=4$\sqrt{5}$-x,
在Rt△FMN中,由勾股定理得:FN2=FM2+MN2,
$(4\sqrt{5}-x)^{2}={x}^{2}+(2x)^{2}$,
解得:x=5-$\sqrt{5}$,
∴ME=EF-FM=8-2x=2$\sqrt{5}$-2,
由①得:DK=2,
tan∠MDE=$\frac{ME}{DE}=\frac{KP}{DK}$,
∴$\frac{2\sqrt{5}-2}{4}=\frac{KP}{2}$,
∴KP=$\sqrt{5}$-1,
∵PD=DQ,DK⊥PQ,
∴PQ=2KP=2$\sqrt{5}$-2,
∴S△PDQ=$\frac{1}{2}$PQ•DK=$\frac{1}{2}$(2$\sqrt{5}$-2)×2=2$\sqrt{5}$-2,
综上所述,重叠部分△DPQ的面积是$\frac{5}{2}$或2$\sqrt{5}$-2;
故答案为:$\frac{5}{2}$或2$\sqrt{5}$-2.
点评 此题主要考查了旋转的性质以及相似三角形的性质和勾股定理等知识,等腰三角形的定义采用分情况讨论的方式,作辅助线,构建直角三角形,利用勾股定理得出方程是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
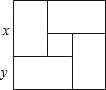 用四个全等的矩形和一个小正方形拼成如图所示的大正方形.已知大正方形的面积是196,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则下列关系式中不正确的是( )
用四个全等的矩形和一个小正方形拼成如图所示的大正方形.已知大正方形的面积是196,小正方形的面积是4,若用x,y表示矩形的长和宽(x>y),则下列关系式中不正确的是( )| A. | x+y=14 | B. | x-y=2 | C. | xy=48 | D. | x2+y2=144 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 南边,-1.5km | B. | 北边、-1.5km | C. | 南边、1.5km | D. | 北边、1.5km |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
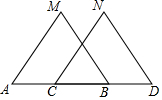 如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )| A. | ∠M=∠N | B. | AM∥CN | C. | AB=CD | D. | AM=CN |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com