
【题目】把多项式2x2﹣5x+x2+4x﹣3x2合并同类项后所得的结果是( )
A.二次二项式
B.二次三项式
C.一次二项式
D.单项式
科目:初中数学 来源: 题型:
【题目】某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地面积占林地面积的20%.设把x公顷旱地改为林地,则可列方程( )
A.54﹣x=20%×108
B.54﹣x=20%(108+x)
C.54+x=20%×162
D.108﹣x=20%(54+x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.

(1)求证:OE=OF.
(2)当∠DOE等于 度时,四边形BFDE为菱形。(直接填写答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:

(1)∠BAE的度数;
(2)∠DAE的度数;
(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B-∠C=40°,也能得出∠DAE的度数?若能,请你写出求解过程;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
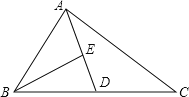
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为40,BD=5,则点E到BC边的距离为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值。如对于任意正实数![]() 、x,可作变形:x+=(-
、x,可作变形:x+=(-![]() )2+2,因为(-
)2+2,因为(-![]() )2≥0,所以x+≥2(当x=时取等号).
)2≥0,所以x+≥2(当x=时取等号).
记函数y=x+(a>0,x>0),由上述结论可知:当x=时,该函数有最小值为2.
直接应用: 已知函数y1=x(x>0)与函数y2 = (x>0),则当x= 时,y1+y2取得最小值为 .
变形应用: 已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>-1),求 的最小值,并指出取得该最小值时相应的x的值.
实际应用:汽车的经济时速是指汽车最省油的行驶速度。某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油(+)升。若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
①、求y关于x的函数关系式(写出自变量x的取值范围);
②、求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市地铁一号与地铁二号线接通后,该市交通通行和转换能力成倍增长,该工程投资预算约为930000万元,这一数据用科学记数法表示为( )
A.9.3×105万元
B.9.3×106万元
C.0.93×106万元
D.9.3×104万元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把代数式xy2﹣9x分解因式,结果正确的是( )
A. x(y2﹣9) B. x(y+3)2 C. x(y+3)(y﹣3) D. x(y+9)(y﹣9)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com