
����Ŀ����֪����ƽ��ֱ������ϵ�У�������![]() ��
��![]() ����x����A��B���㣬��y���ڵ�C���ҶԳ���Ϊֱ��x=�D2 .
����x����A��B���㣬��y���ڵ�C���ҶԳ���Ϊֱ��x=�D2 .
��1����������ߵĽ���ʽ������D�����ꣻ
��2������P(0,t)��y���ϵ�һ�����㣬���������̽����
̽��һ����ͼ1�����PAD�����ΪS����W��t��S����0��t��4ʱ��W�Ƿ������ֵ������У����W�����ֵ�ʹ�ʱt��ֵ�����û�У�˵�����ɣ�
̽��������ͼ2���Ƿ������P��A��DΪ�������������Rt��AOC���ƣ�������ڣ����P�����ꣻ��������ڣ���˵�����ɣ�
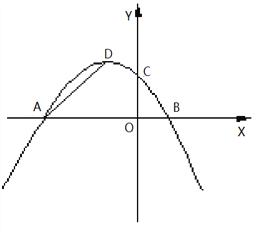

ͼ1 ͼ2
���𰸡���1��y��![]() x2x+3��D��-2��4������2������t=3ʱ��W�����ֵ��W���ֵ=18�������ڣ�ֻ����һ��P��0��2��ʹRt��ADP��Rt��AOC���ƣ�
x2x+3��D��-2��4������2������t=3ʱ��W�����ֵ��W���ֵ=18�������ڣ�ֻ����һ��P��0��2��ʹRt��ADP��Rt��AOC���ƣ�
�������������������1������������y=ax2+bx+c��a��0���Գ�����ֱ��x=![]() ������֪������
������֪������![]() ��
��![]() ���ĶԳ���Ϊֱ��x=�D2����
���ĶԳ���Ϊֱ��x=�D2����![]() ������� a��ֵ������д�������ߵĽ���ʽ�Ͷ������ꣻ��2��̽��һ����������
������� a��ֵ������д�������ߵĽ���ʽ�Ͷ������ꣻ��2��̽��һ����������![]() �Ľ���ʽ����x��y��Ľ���
�Ľ���ʽ����x��y��Ľ���![]() �����꣬��
�����꣬��![]() ����M����
����M����![]() ����
����![]() ����
����![]() ��
��![]()
![]()
![]() �ɵã�
�ɵã�![]() ����
����![]() ʱ��W�����ֵ��
ʱ��W�����ֵ��![]() ��̽�������������������������
��̽�������������������������![]() ʱ����
ʱ����![]() ����E����
����E����![]() ����
����![]() ����
����![]() ����
����![]() ������Ϊ
������Ϊ![]() �ᣬ
�ᣬ![]() �ᣬ��
�ᣬ��![]() ����
����![]() ��
��![]() ��
��![]() �����ʱ��
�����ʱ�� ������Ϊ
������Ϊ![]() ����
����![]() ����ʱ
����ʱ![]() ����
����![]() �����Ե�
�����Ե�![]() ʱ�����ڵ�P1��ʹ
ʱ�����ڵ�P1��ʹ![]() ����ʱP1�������Ϊ��0��2��������
����ʱP1�������Ϊ��0��2��������![]() ʱ����
ʱ����![]() ����
����![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() ������
������![]() ��
��![]() �����ƣ���ʱ��P2�����ڣ�����
�����ƣ���ʱ��P2�����ڣ�����![]() ʱ����ADΪֱ��������
ʱ����ADΪֱ��������![]() �İ뾶
�İ뾶![]() ��Բ��O1��y��ľ���
��Բ��O1��y��ľ���![]() ����Ϊ
����Ϊ![]() ������
������![]() ��y�����룬�����ڵ�P3��ʹ
��y�����룬�����ڵ�P3��ʹ![]() ,
,
�����ۺϿɵã�ֻ����һ��![]() ʹ
ʹ![]() ��
��![]() ���ơ�
���ơ�
���������
��1����������![]() �ĶԳ���Ϊֱ��
�ĶԳ���Ϊֱ��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��2��̽��һ����![]() ʱ��W�����ֵ��
ʱ��W�����ֵ��
��������![]() ��x����A��B���㣬��y���ڵ�C��
��x����A��B���㣬��y���ڵ�C��
��![]() ��
��
��![]() ��
��
��![]() ʱ����
ʱ����![]() ����M����ͼ��ʾ��
����M����ͼ��ʾ��

��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]()
![]() ��
��![]()
![]()
��![]()
����![]() ʱ��W�����ֵ��
ʱ��W�����ֵ��![]() ��
��
̽���������ڣ������������
����![]() ʱ����
ʱ����![]() ����E����ͼ��ʾ��
����E����ͼ��ʾ��
��![]() ��
��
��![]()
��![]() ��
��
��![]()
��![]() �ᣬ
�ᣬ![]() �ᣬ
�ᣬ
��![]() ��
��
��![]() ��
��
��![]()
��![]() ����
����
��ʱ ������Ϊ
������Ϊ![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
����![]() ʱ�����ڵ�P1��ʹ
ʱ�����ڵ�P1��ʹ![]() ����ʱP1�������Ϊ��0��2����
����ʱP1�������Ϊ��0��2����
����![]() ʱ����
ʱ����![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() �����ƣ���ʱ��P2�����ڣ�
�����ƣ���ʱ��P2�����ڣ�
����![]() ʱ����ADΪֱ��������
ʱ����ADΪֱ��������![]() �İ뾶
�İ뾶![]() ��Բ��O1��y��ľ���
��Բ��O1��y��ľ���![]() ����
����![]() ��
��
��![]() ��y�����룬�����ڵ�P3��ʹ
��y�����룬�����ڵ�P3��ʹ![]() ��
��
������������ֻ����һ��![]() ʹ
ʹ![]() ��
��![]() ���ơ�
���ơ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A=40�㣺 
��1����ͼ��1��BO��CO�ǡ�ABC���ڽǽ�ƽ���ߣ����ཻ�ڵ�O�����BOC�� 
��2����ͼ��2��BO��CO�ǡ�ABC����ǽ�ƽ���ߣ����ཻ�ڵ�O�����BOC�� 
��3����ͼ��3��BO��CO�ֱ��ǡ�ABC��һ�ڽǺ�һ��ǽ�ƽ���ߣ����ཻ�ڵ�O�����BOC��
��4�������������ʵĽ��������A=n��ʱ���ֱ���Եó���BOC���A��������������ϵ��ֻ��д�����ۣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ������C��AB���ӳ����ϣ�CD����O�����ڵ�D��CE��AD����AD���ӳ����ڵ�E��
��1����֤����BDC=��A��
��2����CE=4��DE=2����AD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC��ֱ������ϵ�У� 
��1����д����ABC��������꣮
��2�����ѡ�ABC����ƽ��2����λ��������ƽ��1����λ�õ���A��B��C�䣬д��A�䡢B�䡢C������꣮
��3�����������ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽����Ӧ�ã�
��1������д�±���ͨ���۲���ڻش����⣺
�ٱ�����x=��y=��
�ڴӱ�����̽��a�� ![]() ����λ�Ĺ��ɣ�������������ɽ�������������⣺
����λ�Ĺ��ɣ�������������ɽ�������������⣺
��֪ ![]() =1.8����
=1.8���� ![]() =180����a= ��
=180����a= ��
��֪ ![]() =5.036��
=5.036�� ![]() =15.906����
=15.906���� ![]() = ��
= ��
a | �� | 0.0001 | 0.01 | 1 | 100 | 10000 | �� |
| �� | 0.01 | x | 1 | y | 100 | �� |
��2���Ķ����⣬Ȼ��ش����⣻
���⣺��a��b����������������a+ ![]() b=3��2
b=3��2 ![]() ����a+b��ֵ��
����a+b��ֵ��
�⣺������ã�a��3��+��b+2�� ![]() =0����Ϊa��b����������������a��3��b+2Ҳ��������������
=0����Ϊa��b����������������a��3��b+2Ҳ�������������� ![]() ��������������a��3=0��b+2=0������a=3��b=��2������a+b=3+����2��=��1��
��������������a��3=0��b+2=0������a=3��b=��2������a+b=3+����2��=��1��
���⣺��x��y������������������x2��2y+ ![]() y=10+3
y=10+3 ![]() ����xy��ֵ��
����xy��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ȫ����·�����ÿ�Լ41000000�˴Σ���41000000�ÿ�ѧ��������ʾΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ȥ��3m����5m2��3m��5��ʽ���ǣ� ��
A.5��m2��1��
B.5m2��6m��5
C.5��m2+1��
D.����5m2+6m��5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬��E��AC�ϵĵ㣬�ҡ�1=��2��DE��ֱƽ��AB��������D�����EC=3cm����AE���ڣ� �� 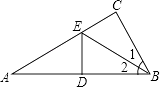
A.3cm
B.4cm
C.6cm
D.9cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ACB���ECD���ǵ���ֱ�������Σ���ACB�Ķ���A�ڡ�ECD��б��DE�ϣ���֤��AE2+AD2=2AC2 �� ����ʾ������BD�� 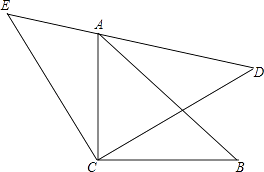
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com