
| A. | 2 | B. | -2 | C. | -1 | D. | 0 |
分析 k<0,函数y=kx2+(k+2)x+5开口向下,再求出对称轴为:x=-$\frac{k+2}{2k}$=-$\frac{1}{2}$-$\frac{1}{k}$>-$\frac{1}{2}$,根据x<m时,y随x的增大而增大,利用二次函数的增减性即可求出m的最大整数值是-1.
解答 解:对于任意负实数k,函数y=kx2+(k+2)x+5的图象是开口向下的抛物线,
对称轴为:x=-$\frac{k+2}{2k}$=-$\frac{1}{2}$-$\frac{1}{k}$>-$\frac{1}{2}$,
∵当x<m时,y随x的增大而增大,
∴m的最大整数值是-1.
故选C.
点评 本题考查了二次函数的性质.掌握二次函数的增减性是解题的关键.


科目:初中数学 来源: 题型:解答题
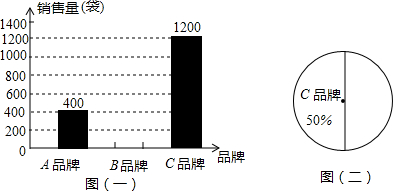
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
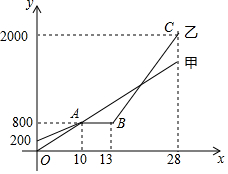 甲、乙相约去离家2000m的公园晨练,甲先出发一直匀速前行,乙后出发,如图是甲和乙所走的路程s(m)与时间t(min)的函数图象.
甲、乙相约去离家2000m的公园晨练,甲先出发一直匀速前行,乙后出发,如图是甲和乙所走的路程s(m)与时间t(min)的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
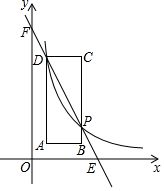 如图,矩形ABCD中,点A(1,1)、B(3,1),C(3,6),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,且与BC交于点P.
如图,矩形ABCD中,点A(1,1)、B(3,1),C(3,6),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,且与BC交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 2$\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
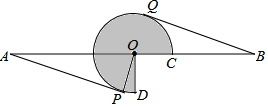 如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧$\widehat{CD}$于点P,Q,且点P,Q在AB异侧,连接OP.
如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧$\widehat{CD}$于点P,Q,且点P,Q在AB异侧,连接OP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com