
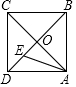
 如图,正方形ABCD的边长为a,AC与BD交于点O,E为OD中点,动点P从点O出发,沿折O→E→A→B→O的路径运动,回到点O时运动停止.设点P运动的路程长为x,AP长为y,则y关于x的函数图象大致是 ( )
如图,正方形ABCD的边长为a,AC与BD交于点O,E为OD中点,动点P从点O出发,沿折O→E→A→B→O的路径运动,回到点O时运动停止.设点P运动的路程长为x,AP长为y,则y关于x的函数图象大致是 ( )| A. | 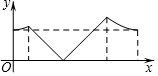 | B. |  | ||
| C. |  | D. | 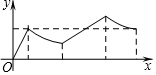 |
分析 根据题意设出点P运动的路程x与点P到点A的距离y的函数关系式,然后对点P在不同线段上时分别进行分析,并写出分段函数,结合图象得出答案.
解答 解:∵正方形ABCD的边长为a,
∴BD=$\sqrt{2}$a,AC⊥BD,
∴OD=$\frac{\sqrt{2}a}{2}$,
∵E为OD中点,
∴OE=$\frac{\sqrt{2}}{4}$a,
当点P在OE上时,
∵OP=x,OA=$\frac{\sqrt{2}}{2}$a,
∴y=$\sqrt{{x}^{2}+\frac{1}{2}{a}^{2}}$,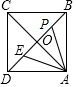
当点P在AE上时,
在Rt△AOE中,AE=$\sqrt{(\frac{\sqrt{2}}{2}a)^{2}+(\frac{\sqrt{2}}{4}a)^{2}}$=$\frac{\sqrt{10}}{4}$a,
∴y=$\frac{\sqrt{10}}{4}a+\frac{\sqrt{2}}{4}a$-x=-x+$\frac{\sqrt{10}+\sqrt{2}}{4}$a;
当点P在AB上时,
∴y=x-$\frac{\sqrt{10}+\sqrt{2}}{4}$a,
当点P在OB上时,
∵OP=$\frac{\sqrt{2}}{2}$a+a+$\frac{\sqrt{10}+\sqrt{2}}{4}$a+$\frac{\sqrt{2}}{4}$a-x=$\frac{\sqrt{10}+4\sqrt{2}}{4}$a-x,
∴y=$\sqrt{O{A}^{2}+O{P}^{2}}$=$\sqrt{\frac{1}{2}{a}^{2}+(\frac{\sqrt{10}+4\sqrt{2}}{4}a-x)^{2}}$,
合函数解析式可以得出第1,4段函数的图象是开口向上的抛物线,第2,3段函数的图象是直线,故只有A符合要求,
故选:A.
点评 此题主要考查了动点问题的函数图象问题;根据自变量不同的取值范围得到相应的函数关系式是解决本题的关键.


科目:初中数学 来源: 题型:解答题
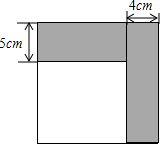 如图所示,小明将一张正方形纸片剪去一条宽为4cm的长条后,再从剩下的长方形纸片上剪去一条宽为5cm的长条.如果两次剪下的长条面积正好相等.
如图所示,小明将一张正方形纸片剪去一条宽为4cm的长条后,再从剩下的长方形纸片上剪去一条宽为5cm的长条.如果两次剪下的长条面积正好相等.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 各有一个角是45°的两个等腰三角形 | |
| B. | 两个等边三角形 | |
| C. | 各有一个角是45°,腰长都是3cm的两个等腰三角形 | |
| D. | 腰和顶角对应相等的两个等腰三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 托盘B与点O的距离x(cm) | 10 | 15 | 20 | 25 | 30 |
| 托盘B中的砝码质量y(g) | 30 | 20 | 15 | 12 | 10 |
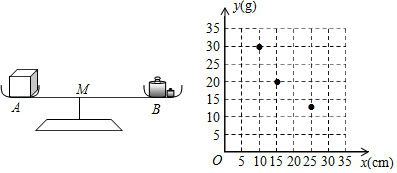
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2xy与-3ab | B. | $\frac{1}{5}$abc与$\frac{1}{5}$ac | C. | xy与-xy | D. | 3x2y与3xy2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在菱形ABCD中,AB=4,对角线AC、BD交于O点,E为AD延长线上一点,DE=2,直线OE分别交AB、CD于G、F.
如图,在菱形ABCD中,AB=4,对角线AC、BD交于O点,E为AD延长线上一点,DE=2,直线OE分别交AB、CD于G、F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com