练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在一次活动中，主办方共准备了3600盆甲种花和2900盆乙种花，计划用甲、乙两种花搭造出A、B两种园艺造型共50个，搭造要求的花盆数如下表所示：

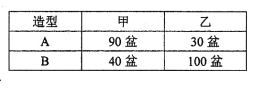
    请问符合要求的搭造方案有几种？请写出具体的方案。

    【答案】符合要求的搭造方案有3种；所有可行的方案有：

    （1）A：30 个 B：20个

    （2）A：31个 B：19个

    （3）A：32个 B：18个

    【解析】

    可设A园艺造型x个，则B园艺造型（50-x）个，根据题意列出关于x的不等式组，由不等式组的解集确定符合要求的搭造方案即可.

    解：设A园艺造型x个，B园艺造型（50-x）个，由题意可得:

    解不等式①得x≤32，

    解不等式②得x≥30

    ∴原不等式组的解集是30≤x≤32

    ∴符合要求的搭造方案有3种

    所以，所有可行的方案有：

    A：30 个 B：20个

    A：31个 B：19个

    A：32个 B：18个

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，∠ABC=90°，AB=3，BC=4，DC=12，AD=13，求四边形ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形OABC的顶点A、C分别在x轴和y轴上，顶点B的坐标为（n，2），点E是AB的中点，在OA上取一点D，将△BAD沿BD翻折，点A刚好落在BC边上的F处，BD、EF交于点P

    （1）直接写出点E、F的坐标；

    （2）若OD=1，求P点的坐标；

    （3）动点Q从P点出发，依次经过F，y轴上的点M，x轴上的点N，然后返回到P点：

    ①若要使Q点运动一周的路径最短，试确定M、N的位置；

    ②若n=3，求最短路径的四边形PFMN的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】你知道古代数学家怎样解一元二次方程吗？以x2﹣2x﹣3=0为例，大致过程如下：第一步：将原方程变形为x2﹣2x=3，即x（x﹣2）=3．

    第二步：构造一个长为x，宽为（x﹣2）的长方形，长比宽大2，且面积为3，如图所示．

    第三步：用四个这样的长方形围成一个大正方形，中间是一个小正方形，如图所示．

    第四步：计算大正方形面积用x表示为　　 　　．长方形面积为常数　　 ．小正方形面积为常数　　 ．

    由观察可得，大正方形面积等于四个长方形与小正方形面积之和，得方程　　 　，两边开方可求得：x1=3，x2=﹣1．

    （1）第四步中横线上应填入　　 　　；　　 　　；　　 　　；　　 　　．

    （2）请参考古人的思考过程，画出示意图，写出步骤，解方程x2﹣x﹣1=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我国古代伟大的数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形，得到一个恒等式．后人借助这种分割方法所得的图形证明了勾股定理，如图所示的矩形由两个这样的图形拼成，若a=3，b=4，则该矩形的面积为（ ）

    A. 20 B. 24 C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知某市2016年企业用水量x（吨）与该月应交的水费y（元）之间的函数关系如图．

    （1）当x≥50时，求y关于x的函数关系式；

    （2）若某企业2016年10月份的水费为620元，求该企业2016年10月份的用水量；

    （3）为鼓励企业节约用水，该市自2017年1月开始对月用水量超过80吨的企业加收污水处理费，规定：若企业月用水量x超过80吨，则除按2016年收费标准收取水费外，超过80吨的部分每吨另加收元的污水处理费，若某企业2017年3月份的水费和污水处理费共600元，求这个企业3月份的用水量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担．李明按照相关政策投资销售本市生产的一种新型节能灯．已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y（件）与销售单价x（元）之间的关系近似满足一次函数:y=-10x+500．

    （1）李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?

    （2）设李明获得的利润为W（元）,当销售单价定为多少元时,每月可获得最大利润?

    （3）物价部门规定,这种节能灯的销售单价不得高于25元．如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店销售一种销售成本为每千克30元的水产品，据市场分析，若按每千克40元销售，一个月能售出500千克；销售单价每涨1元，月销售量就减少10千克，针对这种情况，请解答以下问题：

    （1）当销售单价定为每千克45元时，计算月销售量和月销售利润；

    （2）该商店想在月销售成本不超过10000元的情况下，使得月销售利润达到8000元，销售单价应定为多少?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解居民月用水量，某市对某区居民用水量进行了抽样调查，并制成如下直方图．

    (1)这次一共抽查了____户；

    (2)用水量不足10吨的有____户，用水量超过16吨的有____户；

    (3)假设该区有8万户居民，估计用水量少于10吨的有多少户？

    查看答案和解析>>

    同步练习册答案