
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ᣬy��ֱ��ڵ�A(��4��0)��B(0��3)������P�ӵ�O��������x�Ḻ������ÿ��1����λ���ٶ��˶���ͬʱ����Q�ӵ�B������������BO������ÿ��2����λ���ٶ��˶�������P��PC��AB�ڵ�C������PQ��CQ����PQ��CQΪ�ڱ߹���ƽ���ı���PQCD�����P�˶���ʱ��Ϊt�룮
(1)����Q���߶�OB��ʱ���ú�t�Ĵ���ʽ��ʾPC��AC�ij���
(2)���˶������У�
�ٵ���D����x����ʱ���������������t��ֵ��
������D������ABO�ڲ�(�������߽�)ʱ��ֱ��д��t��ȡֵ��Χ��
(3)����Q����x��ĶԳƵ�Q��������CQ�������˶������У��Ƿ����ijʱ��ʹ��A��P��C�����Բ����CQQ�������е�һ�������У������ڣ������t��ֵ���������ڣ���˵�����ɣ�



���𰸡���1��PC��![]() (4��t)��AC��
(4��t)��AC��![]() (4��t)����2����
(4��t)����2����![]() ����
����![]() ����3�����ڣ�
����3�����ڣ�![]() ��
��![]()
�������������������1���������AB����Rt��ACP��PA=4-t������sin��OAB=![]() �����PC������cos��OAB=
�����PC������cos��OAB=![]() �����AC��
�����AC��
��2�����ٵ�D��x����ʱ����QC��OA����![]() ���ɴ˼��ɽ�����⣮
���ɴ˼��ɽ�����⣮
�ڵ���D��AB��ʱ����PQ��AB����![]() �����ʱ��t������٢���������ʱ�ġ�POQ��������ɽ�����⣮
�����ʱ��t������٢���������ʱ�ġ�POQ��������ɽ�����⣮
��3����QC���M����ʱ����QC��CM������֤��QB=QC����QN��BC��N������cos��ABO=![]() ���г����̼��ɽ�����⣬��CQ���ǡ�M����ʱ���������ƣ�
���г����̼��ɽ�����⣬��CQ���ǡ�M����ʱ���������ƣ�
���������(1)��ͼ1�У�

��OA��8��OB��6����AB��![]() ��5��
��5��
��Rt��ACP��PA��4��t��

��sin��OAB��![]() ����PC��
����PC��![]() (4��t)��
(4��t)��
��cos��OAB��![]() ����AC��
����AC��![]() (4��t)��
(4��t)��
(2)�ٵ�D��x����ʱ����ͼ2�У�
��QC��OA����![]() ��
��![]() ��
��
���![]() ��
��
��![]() ʱ����D��x���ϣ�
ʱ����D��x���ϣ�
��![]() ��
��
(3)��ͼ3�У�

��Q(0��3��2t)��Q��(0��2t��3)��
��QC���M����ʱ����QC��CM��
���QCM��90�㣬���QCP+��PCM��90�㣬�ߡ�QCP+��QCB��90�㣬
���BCQ����PCM����CPM��
�ߡ�CPM+��PAC��90�㣬��OBA+��OAB��90�㣬
���APC����OBA�����QBC����QCB��
��BQ��CQ����QN��BC��N��
��cos��ABO��![]() ����
����![]() ��
��
���![]() ��
��
��CQ���ǡ�M����ʱ��ͬ���ɵ�![]() �����
�����![]() ��
��
��![]() ��
��![]() ʱ����A��P��C�����Բ����CQQ�������е�һ�������У�
ʱ����A��P��C�����Բ����CQQ�������е�һ�������У�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��a��0����ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C����OA=OC�������н��ۣ���abc��0����![]() ����ac��b+1=0����OAOB=��
����ac��b+1=0����OAOB=��![]() ��������ȷ���۵������ ��
��������ȷ���۵������ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����к�����ϵ�У�����������������ϵ���ǣ� ��
A.Բ����������İ뾶
B.���Ϊ����Sʱ���εij�y���x
C.·���dz���ʱ����ʻ���ٶ�v��ʱ��t
D.�����εĵױ��dz���aʱ�������S���������ϵĸ�h
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�������г���ѧ��һ��ʼ��ijһ�㶨���ٶ���ʻ������ʻ��;�����г������˹��ϣ�ֻ��ͣ�����������ú����µ������ϿΣ�������ǰ�ӿ����ﳵ���ٶȣ������ķ�ͼ�����ܷ�ӳС������г̵��ǣ�����������
A.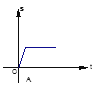
B.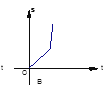
C.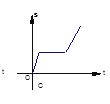
D.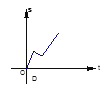
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����Ʒ�ı��۸���200Ԫ�������ż��ڵı仯����Ʒ�ļ۸�ɸ�����10%����һ���10%�ĺ�����ʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����B���߶�AF�ϣ��ֱ���AB��BFΪ�����߶�AF��ͬ����������ABCD��������BFGE������CF��DE��CF��EG�ڵ�H��
(1)��E��BC���е㣬��֤��DE��CF��
(2)����CDE��30�㣬��![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһƽ��ֱ������ϵ����������y=2x2��3��ͼ������ƽ��2����λ��������ƽ��1����λ�õ���ͼ��Ķ��������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬��ABC=30�㣬AB=8������ABC��CB����ƽ�Ƶõ���DEF�����ı���ABED���������8����ƽ�ƾ�����ڣ�������
A.2
B.4
C.8
D.16
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı���ABCD�У�AD��BC�����ı���ABCD��ƽ���ı��Σ���Ӧ����(�� ��)
A. ��A����C��180�� B. ��B����D��180�� C. ��A����B��180�� D. ��A����D��180��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com