
【题目】如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,那么,按照图中所标注的数据,图中实线所围成的图形面积为( ).

A.40.5B.48.5C.50D.52.5
【答案】A
【解析】
由AE⊥AB,EF⊥FH,BG⊥AG,可以得到∠EAF=∠ABG,而AE=AB,∠EFA=∠AGB,由此可以证明△AEF≌△ABG,所以AF=BG,AG=EF;同理证△BGC≌△CHD,得GC=DH,CH=BG,从而得出FH的长度,然后利用梯形DHEF的面积减去△AEF、△ABG、△BGC与△CHD的面积即可得出答案.
因为AE⊥AB,EF⊥FH,BG⊥AG,
所以∠EAF+∠BAG=∠BAG+∠ABG=90°
所以∠EAF=∠ABG
在△AEF与△ABG中
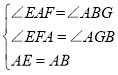
所以△AEF≌△ABG
所以AF=BG=2,AG=EF=6
因为BC⊥CD,DH⊥CH,BG⊥GC,
所以∠BCG+∠DCH=∠DCH+∠CDH=90°
所以∠BCG=∠CDH
在△BGC与△CHD中
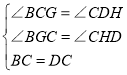
所以△BGC≌△CHD
所以GC=DH=3,CH=BG=2
所以FH=2+6+2+3=13
因为实线所围成的图形面积等于梯形DHEF的面积减去△AEF、△ABG、△BGC与△CHD的面积,
所以![]() ,
,
所以答案选A.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】用一条直线分割一个三角形,如果能分割出等腰三角形,那么就称这条直线为该三角形的一条等腰分割线.在直角三角形ABC中,∠C=90°,AC=8,BC=6.

(1)如图(1),若 O 为 AB 的中点,则直线 OC_____△ABC 的等腰分割线(填“是”或“不是”)
(2)如图(2)已知△ABC 的一条等腰分割线 BP 交边 AC 于点 P,且 PB=PA,请求出 CP 的长度.
(3)如图(3),在△ABC 中,点 Q 是边 AB 上的一点,如果直线 CQ 是△ABC 的等腰分割线,求线段BQ 的长度等于 ______.(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为 1 个单位长度的小正方形组成的网格中,点 A、B、C 在小正方形的顶点上.

(1)在图中画出与△ABC 关于直线 l 成轴对称的△A′B′C′;
(2)连接 AA′,则△ACA′的面积为 ;
(3)在直线 l 上找一点 P,使 PA+PB 的长最短,则这个最短长度为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
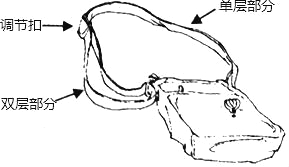
【题目】如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小敏用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
单层部分的长度x(cm) | … | 4 | 6 | 8 | 10 | … | 150 |
双层部分的长度y(cm) | … | 73 | 72 | 71 | … |
(1)根据表中数据的规律,完成以下表格,并直接写出y关于x的函数解析式;
(2)根据小敏的身高和习惯,挎带的长度为120cm时,背起来正合适,请求出此时单层部分的长度;
(3)设挎带的长度为lcm,求l的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=40°,
(1)若点P是∠ABC与∠ACB平分线的交点,求∠P的度数;
(2)若点P是∠CBD与∠BCE平分线的交点,求∠P的度数;
(3)若点P是∠ABC与∠ACF平分线的交点,求∠P的度数;
(4)若∠A=β,求(1)(2)(3)中∠P的度数(用含β的代数式表示,直接写出结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中,装有红球、白球、黄球共12个,这些球除颜色外完全相同,
从中随机摸出一个球,则:
(1)若盒子中有红球3个,则摸到红球的概率为_________;
(2)若摸到黄球的概率为![]() ,则该盒子中装有黄球的个数是__________个;
,则该盒子中装有黄球的个数是__________个;
(3)若将这12个球分别标上1至12这十二个数字,则摸到的数字是0的概率为________;摸到的数字是偶数的概率为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com