
| A. | x6+x6=x12 | B. | (x2)3=x5 | C. | x-1=x | D. | x2•x3=x5 |
科目:初中数学 来源: 题型:选择题
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校为了解全校1600名学生每周课外体育活动时间的情况,随机调查了其中的部分学生,对这些学生每周课外体育活动时间x(单位:小时)进行了统计,根据所得数据绘制了一幅统计图,根据以上信息及统计图解答下列问题
某校为了解全校1600名学生每周课外体育活动时间的情况,随机调查了其中的部分学生,对这些学生每周课外体育活动时间x(单位:小时)进行了统计,根据所得数据绘制了一幅统计图,根据以上信息及统计图解答下列问题查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)
如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
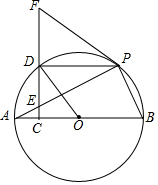 如图.AB是⊙O的直径,E为弦AP上一点,过点E作EC⊥AB于点C,延长CE至点F,连接FP,使∠FPE=∠FEP,CF交⊙O于点D.
如图.AB是⊙O的直径,E为弦AP上一点,过点E作EC⊥AB于点C,延长CE至点F,连接FP,使∠FPE=∠FEP,CF交⊙O于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com