Question

17．如图1，正方形ABCD，E、F分别为BC、AB中点，求$\frac{AM}{EM}$．
如图2，正六边形ABCDEF，M为CD中点，点N在BC上，CN=2BN，AM、FN相交于P，求$\frac{AP}{PM}$．
如图3，M为CD中点，EH⊥AM交BC于H，若正六边形边长为4，求CH的长．

Answer 1

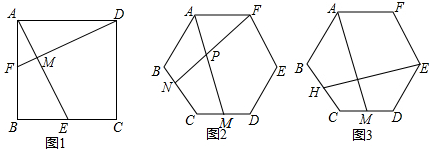
分析 （1）如图1中，设正方形ABCD的边长为2a．首先证明AE⊥DF，想办法求出AM、EM即可解决问题；
（2）如图2中，延长AB交DC的延长线于G，连接FG交BC于N′，作BE∥AF交EG于E．只要证明N与N′重合即可解决问题；
（3）如图3中，建立如图坐标系．（C为坐标原点，CD为x轴，CA为y轴）．求出直线BC、EH的解析式，利用方程组求出解得H的坐标即可解决问题；

解答 解：（1）如图1中，设正方形ABCD的边长为2a．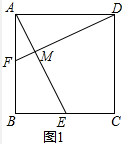

∵AD=AB，∠DAF=∠B=90°，AF=BE，
∴△DAF≌△BAE，
∴∠ADF=∠BAE，
∵∠BAE+∠EAD=90°，
∴∠EAD+∠ADF=90°，
∴∠AMD=90°，
∴AE⊥DF，
∵DF=AE=$\sqrt{（2a）^{2}+{a}^{2}}$=$\sqrt{5}$a，
$\frac{1}{2}$•AF•AD=$\frac{1}{2}$•DF•AM，
∴AM=$\frac{2\sqrt{5}}{5}$a，EM=$\sqrt{5}$a-$\frac{2\sqrt{5}}{5}$a=$\frac{3\sqrt{5}}{5}$，
∴$\frac{AM}{EM}$=$\frac{2}{3}$．

（2）如图2中，延长AB交DC的延长线于G，连接FG交BC于N′，作BE∥AF交EG于E．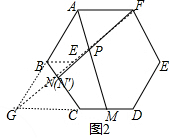

∵ABCDEF是正六边形，
∴∠ABC=∠BCD=120°，
∴∠GBC=∠GCB=60°，
∴GBC是等边三角形，
∴BC=BG=AB=CG，
∵BE∥AF，
∴ME=EF，
∵BE：AF=1：2，
∵CG=AF，
∴BE：CG=BN′：CN′=1：2，
∵CN=2BN，
∴N与N′重合，设AF=CD=2m则GM=3a，
∵AF∥GM，
∴$\frac{AP}{PM}$=$\frac{AF}{GM}$=$\frac{2}{3}$．

（3）如图3中，建立如图坐标系．（C为坐标原点，CD为x轴，CA为y轴）．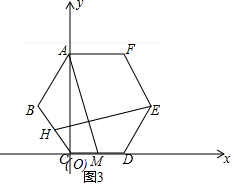

易知M（3，0），A（0，6$\sqrt{3}$），E（9，3$\sqrt{3}$），B（-3，3$\sqrt{3}$），
∴直线AM的解析式为y=-2$\sqrt{3}$x+6$\sqrt{3}$，
直线BC的解析式为y=-$\sqrt{3}$x，
∵AM⊥HE
∴直线HE的解析式为y=$\frac{\sqrt{3}}{6}$x+$\frac{3\sqrt{3}}{2}$，
由$\left\{\begin{array}{l}{y=-\sqrt{3}x}\\{y=\frac{\sqrt{3}}{6}x+\frac{3\sqrt{3}}{2}}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=-\frac{9}{7}}\\{y=\frac{9}{7}\sqrt{3}}\end{array}\right.$，
∴H（-$\frac{9}{7}$，$\frac{9}{7}$$\sqrt{3}$），
∴CH=$\sqrt{（\frac{9}{7}）^{2}+（\frac{9}{7}\sqrt{3}）^{2}}$=$\frac{18}{7}$．

点评 本题考查是那些综合题、正方形的性质、全等三角形的判定和性质、勾股定理、平行线分线段成比例定理、平面直角坐标系、一次函数的应用等知识，解题的关键是学会添加常用辅助线，学会构建平面直角坐标系解决问题，属于中考压轴题．