
【题目】如图1,已知线段AB、CD相交于点O,连接AC、BD,我们把形如图1的图形称之为“8字形”.如图2,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)仔细观察,在图2中有 个以线段AC为边的“8字形”
(2)在图2中,若∠B=96°,∠C=100°,求∠P的度数.
(3)在图2中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
∠CDB,试问∠P与∠D、∠B之间存在着怎样的数量关系(用α、β表示∠P),并说明理由;
(4)如图3,则∠A+∠B+∠C+∠D+∠E+∠F的度数为
【答案】
(1)3
(2)
解:∵∠CAB和∠BDC的平分线AP和DP相交于点P,
∴∠CAP=∠BAP,∠BDP=∠CDP,
∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,
∴∠C﹣∠P=∠P﹣∠B,
即∠P=![]() (∠C+∠B),
(∠C+∠B),
∵∠C=100°,∠B=96°
∴∠P=![]() (100°+96°)=98°;
(100°+96°)=98°;
(3)
解:∠P=![]() (β+2α);
(β+2α);
理由:∵∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,
∠CDB,
∴∠BAP=![]() ∠BAC,∠BDP=
∠BAC,∠BDP=![]() ∠BDC,
∠BDC,
∵∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,
∴∠C﹣∠P=![]() ∠BDC﹣
∠BDC﹣![]() ∠BAC,∠P﹣∠B=
∠BAC,∠P﹣∠B=![]() ∠BDC﹣
∠BDC﹣![]() ∠BAC,
∠BAC,
∴2(∠C﹣∠P)=∠P﹣∠B,
∴∠P=![]() (∠B+2∠C),
(∠B+2∠C),
∵∠C=α,∠B=β,
∴∠P=![]() (β+2α);
(β+2α);
(4)3600
【解析】(1)以M为交点的“8字形”有1个,以O为交点的“8字形”有2个;
(2)根据角平分线的定义得到∠CAP=∠BAP,∠BDP=∠CDP,再根据三角形内角和定理得到∠CAP+∠C=∠CDP+∠P,∠BAP+∠P=∠BDP+∠B,两等式相减得到∠C﹣∠P=∠P﹣∠B,即∠P=![]() (∠C+∠B),然后把∠C=100°,∠B=96°代入计算即可;
(∠C+∠B),然后把∠C=100°,∠B=96°代入计算即可;
(3)与(2)的证明方法一样得到∠P=![]() (2∠C+∠B).
(2∠C+∠B).
(4)根据三角形内角与外角的关系可得∠B+∠A=∠1,∠C+∠D=∠2,再根据四边形内角和为360°可得答案.
【考点精析】关于本题考查的三角形的内角和外角和多边形内角与外角,需要了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°才能得出正确答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(1)请在横线上填写合适的内容,完成下面的证明:
如图1,AB∥CD,求证:∠B+∠D=∠BED.
证明:过点E引一条直线EF∥AB
∴∠B=∠BEF,( )
∵AB∥CD,EF∥AB
∴EF∥CD( )
∴∠D=( )
∴∠B+∠D=∠BEF+∠FED
即∠B+∠D=∠BED.
(2)如图2,AB∥CD,请写出∠B+∠BED+∠D=360°的推理过程.
(3)如图3,AB∥CD,请直接写出结果∠B+∠BEF+∠EFD+∠D= 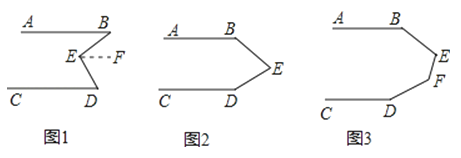
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论中,不正确的是( )
A. 两点确定一条直线
B. 两点之间,直线最短
C. 等角的余角相等
D. 过直线外一点,有且只有一条直线与已知直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题的是( )
A.平行四边形的对角线一定相等
B.等腰三角形任意一条边上的高线、中线和角平分线都三线合一
C.三角形的中位线平行于第三边并且等于它的一半
D.三角形的两边之和小于第三边
查看答案和解析>>
科目:初中数学 来源: 题型:
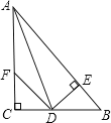
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
证明:(1)CF=EB.
(2)AB=AF+2EB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com