
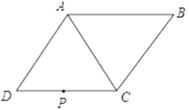
【题目】如图,在菱形ABCD中,∠ADC=60°,CD=4![]() cm,P为CD的中点.
cm,P为CD的中点.
(1)在AC上找一点Q,使DQ+PQ的值最小(保留画图痕迹,不写画法,不必说理);
(2)求出(1)中DQ+PQ的长.
【答案】(1)见解析;(2)2![]() cm
cm
【解析】
(1)如图,连接 PB 交 AC 于点 Q,点 Q 是所求作的;
(2)连接 PA.证明△PAB 是直角三角形,利用勾股定理求出 PB 即可;
解:(1)如图,连接 PB 交 AC 于点 Q,点 Q 是所求作的;
(2)连结 AP,

在菱形 ABCD 中,AB=AD=CD=4![]() cm,又∵∠ADC=60°,
cm,又∵∠ADC=60°,
∴△ACD 为等边三角形,
∵P 为 CD 的中点,
AP⊥CD,DP= ![]() CD=2
CD=2![]() cm, 在 Rt△ADP 中,
cm, 在 Rt△ADP 中,
∴AP=![]()
![]() =6(cm),
=6(cm),
∵AP⊥CD,AB∥CD,
∴AP⊥AB,
在 Rt△ABP 中,BP=![]() =
=![]() (cm),
(cm),
在菱形 ABCD 中,AC⊥BD,OB=OD
∴DQ=BQ
∴DQ+PQ=BQ+PQ=BP=2![]() (cm).
(cm).
答:DQ+PQ 的长为 2![]() cm.
cm.


科目:初中数学 来源: 题型:
【题目】如图1,已知二次函数![]() (
(![]() 为常数,
为常数,![]() )的图象过点
)的图象过点![]() 和点
和点![]() ,函数图象最低点
,函数图象最低点![]() 的纵坐标为
的纵坐标为![]() .直线
.直线![]() 的解析式为
的解析式为![]()
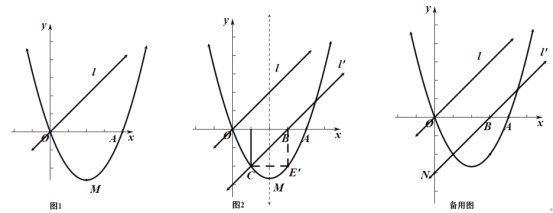
![]() 求二次函数的解析式;
求二次函数的解析式;
![]() 直线
直线![]() 沿
沿![]() 轴向右平移,得直线
轴向右平移,得直线![]() ,
,![]() 与线段
与线段![]() 相交于点
相交于点![]() ,与
,与![]() 轴下方的抛物线相交于点
轴下方的抛物线相交于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,把
,把![]() 沿直线
沿直线![]() 折叠,当点
折叠,当点![]() 恰好落在抛物线上点
恰好落在抛物线上点![]() 时(图
时(图![]() 求直线
求直线![]() 的解析式;
的解析式;
![]() 在
在![]() 的条件下,
的条件下,![]() 与
与![]() 轴交于点
轴交于点![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,P为
,P为![]() 上的动点,当
上的动点,当![]() 为等腰三角形时,求符合条件的点
为等腰三角形时,求符合条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6![]() ,那么AC=_____.
,那么AC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
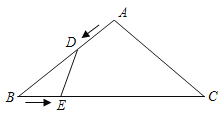
【题目】如图所示,在等腰△ABC中,AB=AC=10cm,BC=16cm.点D由点A出发沿AB方向向点B匀速运动,同时点E由点B出发沿BC方向向点C匀速运动,它们的速度均为1cm/s.连接DE,设运动时间为t(s)(0<t<10),解答下列问题:
(1)当t为何值时,△BDE的面积为7.5cm2;
(2)在点D,E的运动中,是否存在时间t,使得△BDE与△ABC相似?若存在,请求出对应的时间t;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() .
.![]() 于
于![]() .
.![]() 为边
为边![]() 上的一个(不与
上的一个(不与![]() 、
、![]() 重合)点,且
重合)点,且![]() 于
于![]() 相交于点
相交于点![]() .
.

(1)填空:![]() ______;
______;![]() ______.
______.
(2)当![]() 时,证明:
时,证明:![]() .
.
(3)![]() 面积的最小值是_______.
面积的最小值是_______.
(4)当![]() 的内心在
的内心在![]() 的外部时,直接写出
的外部时,直接写出![]() 的范围______.
的范围______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:

若n=24,则第2019次“F”运算的结果是( )
A.4B.1C.2018D.42018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件8元,出厂价为每件10元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3410元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD中,AB=5,BC=8,点P为BC上一动点(不与端点重合),连接AP,将△ABP沿着AP折叠.点B落到M处,连接BM、CM,若△BMC为等腰三角形,则BP的长度为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励城市周边的农民的种菜的积极性,某公司计划新建![]() ,
,![]() 两种温室80栋,将其售给农民种菜.已知建1个
两种温室80栋,将其售给农民种菜.已知建1个![]() 型温室和2个
型温室和2个![]() 型温室一共需要8.1万元,两种温室的成本和出售价如下表:
型温室一共需要8.1万元,两种温室的成本和出售价如下表:
|
| |
成本(万元/栋) | 2.5 |
|
出售价(万元/栋) | 3.1 | 3.5 |
(1)求![]() 的值;
的值;
(2)已知新建![]() 型温室不少于38栋不多于50栋且所建的两种温室可全部售出.为了减轻菜农负担,试问采用什么方案建设温室可使利润最少,最少利润是多少?
型温室不少于38栋不多于50栋且所建的两种温室可全部售出.为了减轻菜农负担,试问采用什么方案建设温室可使利润最少,最少利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com