
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 下表1为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,如图是按照某公司购买的100张门票的种类、数量绘制的扇形图:
下表1为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,如图是按照某公司购买的100张门票的种类、数量绘制的扇形图:| 比赛项目 | 票价(元/张) |
| 足球 | 1000 |
| 男篮 | 800 |
| 乒乓球 | 500 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 摸球的次数n | 200 | 300 | 400 | 500 | 800 | 1000 |
| 摸到白球的次数m | 117 | 186 | 242 | 296 | 483 | 599 |
| 摸到白球的频率 $\frac{n}{m}$ | 0.585 | 0.620 | 0.605 | 0.592 | 0.604 | 0.599 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
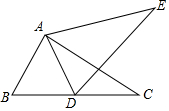 如图,将△ABC绕点A逆时针旋转50°得到△ADE,其中点D恰好落在BC边上,则∠EDC等于( )
如图,将△ABC绕点A逆时针旋转50°得到△ADE,其中点D恰好落在BC边上,则∠EDC等于( )| A. | 40° | B. | 50° | C. | 60° | D. | 65° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com