
已知梯形ABCD, AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,问题:
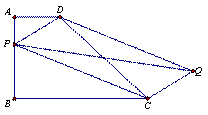
(1)如图1,P为AB边上一点,以PD、PC为边做平行四边形PCQD,请问对角线PQ,DC的长能否相等,为什么?
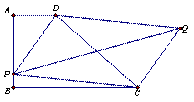
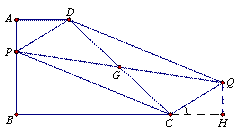
(2)如图2,P为AB边上任意一点,以PD、PC为边做平行四边形PCQD,请问对角线PQ的长是否存在最小值?若果存在,请求出最小值;如果不存在,请说明理由。
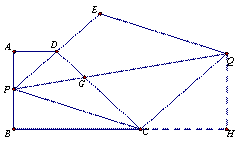
(3)P为AB边上任意一点,延长PD到E,使DE=PD,以PE、PC为边做平行四边形PCQE,请探究对角线PQ的长是否也存在最小值?若果存在,请求出最小值;如果不存在,请说明理由。
(图1) (图2)
(1)问题1:因为四边形PCQD是平行四边形,若对角线PQ、DC相等,则四边形PCQD是矩形。
所以∠DPC=90 ,因为AD=1,AB=2,BC=3.所以DC=2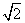 ,设PB=x,则AP=2-x,在Rt△DPC中,PD2+PC2=DC2,即x2+32+ (2-x)2+1=8,化简得x2-2x+3=0,
,设PB=x,则AP=2-x,在Rt△DPC中,PD2+PC2=DC2,即x2+32+ (2-x)2+1=8,化简得x2-2x+3=0,
因为△=(-2)2-4×1×3=-8<0,方程无解,所以对角线PQ与DC不可能相等
(2)问题2:如图1,在平行四边形PCQD中,设对角线PQ与DC相交于点G,所以点G是DC的中点,
作QH⊥BC,交BC的延长线于H。因为AD∥BC,所以∠ADC=∠DCH,即∠ADP+∠PDG=∠DCQ+QCH,
因为PD∥CQ,所以∠PDC=∠DCQ,所以∠ADP=∠QCH,,又PD=CQ,所以Rt△ADP≌Rt△HCQ,所以AD=HC……2分。因为AD=1,BC=3,所以BH=4,所以当PQ⊥AB时,PQ的长最小,即为4。
(3)问题3:如图2,设PQ与DC相较于点G。
因为PE∥CQ,PD=DE,所以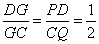 ,所以G是DC上一定点。作QH⊥BC,交BC的延长线于H,同理可证∠ADP=∠QCH,所以Rt△ADP∽Rt△HCQ 即
,所以G是DC上一定点。作QH⊥BC,交BC的延长线于H,同理可证∠ADP=∠QCH,所以Rt△ADP∽Rt△HCQ 即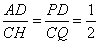 ,所以CH=2. 所以BH=BC+CH=3+2=5,,所以当PQ⊥AB时,PQ的长最小,即为5.
,所以CH=2. 所以BH=BC+CH=3+2=5,,所以当PQ⊥AB时,PQ的长最小,即为5.
(注:各题如有其它解法,只要正确,均可参照给分)
(图1) (图2)


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
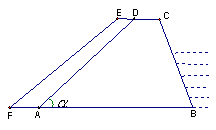
如图,某堤坝的横截面是梯形ABCD,背水坡AD的坡度i(即tan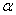 )为1︰1.2,坝高为5米。现为了提高堤坝的防洪抗洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽1米,形成新的背水坡EF,其坡度为1︰1.4。已知堤坝总长度为4000米。
)为1︰1.2,坝高为5米。现为了提高堤坝的防洪抗洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽1米,形成新的背水坡EF,其坡度为1︰1.4。已知堤坝总长度为4000米。
(1)求完成该工程需要多少土方?
(2)该工程由甲、乙两个工程队同时合作完成,按原计划需要20天。准备开工前接到上级通知,汛期可能提前,要求两个工程队提高工作效率。甲队工作效率提高30%,乙队工作效率提高40%,结果提前5天完成。问这两个工程队原计划每天各完成多少土方?
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
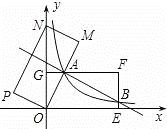
如图,在平面直角坐标系中,矩形OEFG的顶点F的坐标为(4,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴上,得到矩形OMNP,OM与GF相交于点A.若经过点A的反比例函数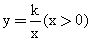 的图象交EF于点B,则点B的坐标为 .
的图象交EF于点B,则点B的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图①,在梯形ABCD中,AD∥BC,∠A=60°,动点P从A点出发,以1cm/s的速度沿着A→B→C→D的方向不停移动,直到点P到达点D后才停止.已知△PAD的面积S(单位:cm2)与点P移动的时间(单位:s)的函数如图②所示,则下列结论:①AB=BC=2cm;②cos∠CDA=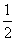 ;③梯形ABCD的面积为
;③梯形ABCD的面积为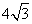 cm2;④点P从开始移动到停止移动一共用了(
cm2;④点P从开始移动到停止移动一共用了(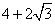 )秒;其中正确的结论是( )。
)秒;其中正确的结论是( )。
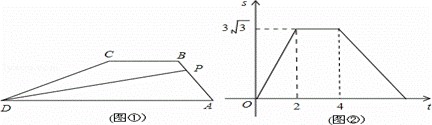
(第10题)
A.①② B.①③ C.①③④ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知:△ABC中,
(1)只用直尺(没有刻度)和圆规求作一点P,使点P同时满足下列两个条件(保留作图痕迹,不必写出作法):①点P到∠CAB的两边距离相等:②点P到A,B两点的距离相等。
(2)若△ABC中,AC = AB = 4,∠CAB=120°,那么请计算以△ABC为轴截面的圆锥的侧面积(保留根号和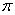 )。
)。
查看答案和解析>>
科目:初中数学 来源: 题型:
有如下四个命题:①三角形有且只有一个内切圆;②四边形的内角和与外角和相等;③顺次连接四边形各边中点所得的四边形一定是菱形;④一组对边平行且一组对角相等的四边形是平行四边形.其中的真命题是( )
A.①②③ B.②④ C.①②④ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
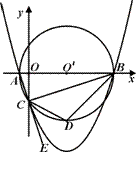
如图,已知点A的坐标是(-1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.
(1)求点C的坐标及抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,求点D的坐标;并直接写出直线BC、直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD,若存在,请求出点P的坐标,若不存在,请说明理由.
 (改编)
(改编)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com