
分析 根据分式的除法和减法可以化简题目中的式子,然后将x4cos30°•sin45°-2化简求值再代入前面分式化简后的式子即可解答本题.
解答 解:$\frac{8x}{{x}^{2}+4x+4}$÷$\frac{{x}^{2}-2x}{{x}^{2}-4}$-$\frac{2}{x+2}$
=$\frac{8x}{(x+2)^{2}}•\frac{(x+2)(x-2)}{x(x-2)}-\frac{2}{x+2}$
=$\frac{8}{x+2}-\frac{2}{x+2}$
=$\frac{6}{x+2}$,
∵x=4cos30°•sin45°-2=4×$\frac{\sqrt{3}}{2}•\frac{\sqrt{2}}{2}$-2=$\sqrt{6}-2$,
∴当a=$\sqrt{6}-2$时,原式=$\frac{6}{\sqrt{6}-2+2}=\frac{6}{\sqrt{6}}=\sqrt{6}$.
点评 本题考查分式的化简求值、特殊角的三角函数值,解答本题的关键是明确分式化简求值的方法和知道特殊角的三角函数值.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
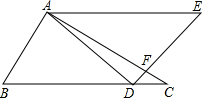 将一副三角板拼成如图所示的图形,即∠BAC=∠ADE=90°,∠DAE=∠E=45°,∠C=30°,∠B=60°,DE与AC相交于点F.
将一副三角板拼成如图所示的图形,即∠BAC=∠ADE=90°,∠DAE=∠E=45°,∠C=30°,∠B=60°,DE与AC相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 这一批零件的质量全体是总体 | |
| B. | 从中抽取的10件零件是总体的一个样本 | |
| C. | 这一批零件的长度的全体是总体 | |
| D. | 每一个零件的质量为个体 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠1=50°,∠2=40° | B. | ∠1=50°,∠2=50° | C. | ∠1=40°,∠2=40° | D. | ∠1=45°,∠2=45° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{3}^{2}}{4}$与$\frac{9}{16}$ | B. | -(-$\frac{1}{3}$)与|-$\frac{1}{3}$| | C. | (-$\frac{1}{3}$)2与-$\frac{1}{9}$ | D. | $\sqrt{\frac{1}{4}}$与$\root{3}{-\frac{1}{8}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com