
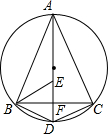
 如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.分析 (1)利用等弧对等弦即可证明.
(2)利用等弧所对的圆周角相等,可得∠BAD=∠CBD,再等量代换得出∠DBE=∠DEB,从而证明DB=DE=DC,所以E,C两点在以D为圆心,DB为半径的圆上.
解答 (1)证明:∵AD为直径,AD⊥BC,
∴$\widehat{BD}$=$\widehat{CD}$,
∴BD=CD.
(2)B,E,C三点在以D为圆心,以DB为半径的圆上.
理由:由(1)知:$\widehat{BD}$=$\widehat{CD}$,
∴∠BAD=∠CBD,
又∵BE平分∠ABC,
∴∠CBE=∠ABE,
∵∠DBE=∠CBD+∠CBE,∠DEB=∠BAD+∠ABE,∠CBE=∠ABE,
∴∠DBE=∠DEB,
∴DB=DE.
由(1)知:BD=CD,
∴DB=DE=DC.
∴E,C两点在以D为圆心,以DB为半径的圆上.
点评 本题主要考查等弧对等弦,及确定一个圆的条件,此类题是中考的常考题,需要同学们牢固掌握.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:解答题
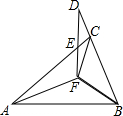 如图,已知△ABF≌△ACF≌△DBF,∠FAB:∠ABF:∠AFB=4:7:25.
如图,已知△ABF≌△ACF≌△DBF,∠FAB:∠ABF:∠AFB=4:7:25.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
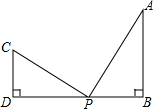 如图:若AB⊥BD,CD⊥BD,动点P在BD上且CP⊥AP,若AB=3,CD=2,BD=7.
如图:若AB⊥BD,CD⊥BD,动点P在BD上且CP⊥AP,若AB=3,CD=2,BD=7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
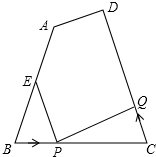 如图,已知四边形ABCD中,AB=10厘米,BC=8厘米,CD=12厘米,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
如图,已知四边形ABCD中,AB=10厘米,BC=8厘米,CD=12厘米,∠B=∠C,点E为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com