
分析 (1)令二次函数解析式中y=0,根据根与系数的关系可得出“x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$”,利用配方法即可求出|x2-x1|的值,由此即可得出结论;
(2)利用配方法将二次函数解析式转化成顶点式,由此即可求出点C的坐标,再根据等腰直角三角形的性质可得出2×|$\frac{4ac-{b}^{2}}{4a}$|=$\frac{\sqrt{{b}^{2}-4ac}}{|a|}$,利用换元解方程即可求出b2-4ac的值;
(3)由(2)的结论即可得出关于k的方程,解方程即可得出抛物线的解析式,画出函数图象,由此可得出若要使∠ACB=60°,则需把抛物线往下平移,设平移的距离为n(n>0),则平移后的抛物线的解析式为y=x2-2$\sqrt{2}$x+1-n,结合(1)(2)的结论即可得出关于n的一元二次方程,解方程即可得出结论.
解答 解:(1)令y=ax2+bx+c(a≠0)中y=0,则有ax2+bx+c=0,
∵二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点为A(x1,0),B(x2,0),
∴x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$,
∴|x2-x1|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{(-\frac{b}{a})^{2}-4×\frac{c}{a}}$=$\frac{\sqrt{{b}^{2}-4ac}}{|a|}$.
(2)∵二次函数y=ax2+bx+c=a$(x+\frac{b}{2a})^{2}$+$\frac{4ac-{b}^{2}}{4a}$,
∴点C的坐标为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),
∵△ABC为等腰直角三角形,
∴2×|$\frac{4ac-{b}^{2}}{4a}$|=$\frac{\sqrt{{b}^{2}-4ac}}{|a|}$,
令$\sqrt{{b}^{2}-4ac}$=m,则有m2-2m=0,
解得:m=2,或m=0,
∵二次函数与x轴有两个不相同的交点,
∴m=$\sqrt{{b}^{2}-4ac}$=2,
∴b2-4ac=4.
(3)∵∠ACB=90°,
∴b2-4ac=k2-4=4,
解得:k=±2$\sqrt{2}$.
选k=-2$\sqrt{2}$,画出图形,如图所示.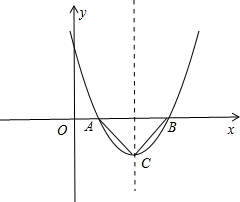
若要使∠ACB=60°,则需把抛物线往下平移,设平移的距离为n(n>0),则平移后的抛物线的解析式为y=x2-2$\sqrt{2}$x+1-n,
由(1)可知AB=$\frac{\sqrt{{b}^{2}-4ac}}{|a|}$=2$\sqrt{1+n}$,
由(2)可知点C(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),即($\sqrt{2}$,-1-n),
∵△ABC为等腰三角形,且∠ACB=60°,
∴-yC=$\frac{\sqrt{3}}{2}$AB,即1+n=$\sqrt{3}$$\sqrt{1+n}$,
解得:n=-1(舍去),或n=2.
故将抛物线往下平移2个单位长度,能使∠ACB=60°.
点评 本题考查了根与系数的关系、等腰直角三角形的性质、等边三角形的性质以及解一元二次方程,解题的关键是:(1)利用配方法求出|x2-x1|的值;(2)利用换元法解方程;(3)根据等边三角形的性质找出关于n的方程.本题属于中档题,难度不大,但解题过程稍显繁琐,解决该题型题目时,利用等腰直角(等边)三角形的性质得出边与边的关系是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
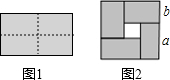 如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积为( )
如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积为( )| A. | ab | B. | (a+b)2 | C. | (a-b)2 | D. | a2-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
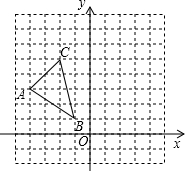 在边长为1个单位长度的小正方形组成的网格中建立如图所示的平面直角坐标系,并给出了格点△ABC(顶点是网格线的交点).
在边长为1个单位长度的小正方形组成的网格中建立如图所示的平面直角坐标系,并给出了格点△ABC(顶点是网格线的交点).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com