Question

19．如图，在梯形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=24cm，BC=26cm，AB为⊙O的直径，动点P从点A开始，沿边AD向点D以1cm/s的速度运动，点Q从点C开始，沿边CB向点B以3cm/s的速度运动，点P、Q分别从点A、C出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒．
（1）当t为何值时，四边形PQCD是平行四边形？
（2）当t为何值时，直线PQ与⊙O相切、相交、相离？

Answer 1

分析 （1）四边形PQCD为平行四边形，即CQ=PD，列出方程求解即可；
（2）因为点P、Q分别在线段AD和BC上的运动，可以统一到直线PQ的运动中，要探求时间t对直线PQ与⊙O位置关系的影响，可先求出t为何值时，直线PQ与⊙O相切这一整个运动过程中的一瞬，再结合PQ的初始与终了位置一起加以考虑，设运动t秒时，直线PQ与⊙O相切于点G，如图因为，AB=8，AP=t，BQ=26-3t，所以，PQ=26-2t，因而，过p做PH⊥BC，得HQ=26-4t，于是由勾股定理，可的关于t的一元二次方程，则t可求．问题得解．

解答 解：设运动时间为t秒，
∴AP=tcm，PD=AD-AP=（24-t）cm，CQ=3tcm，BQ=BC-CQ=（24-2t）cm．
（1）∵AD∥BC，
∴当CQ=PD时，四边形PQCD是平行四边形．
此时有3t=24-t，
解得t=6．
∴当t=6s时，四边形PQCD是平行四边形；
（2）设运动t秒时，直线PQ与⊙O相切于点G，过P作PH⊥BC于点H，
则PH=AB=8，BH=AP，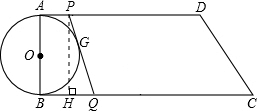
可得HQ=26-3t-t=26-4t，
由切线长定理得，AP=PG，QG=BQ，
则PQ=PG+QG=AP+BQ=t+26-3t=26-2t
由勾股定理得：PQ²=PH²+HQ²，即 （26-2t）²=8²+（26-4t）²
化简整理得 3t²-26t+16=0，
解得t₁=$\frac{2}{3}$或 t₂=8，
所以，当t₁=$\frac{2}{3}$或 t₂=8时直线PQ与⊙O相切．
因为t=0秒时，直线PQ与⊙O相交，
当t=$\frac{26}{3}$秒时，Q点运动到B点，P点尚未运动到D点，但也停止运动，直线PQ也与⊙O相交，
所以可得以下结论：
当t₁=$\frac{2}{3}$或 t₂=8秒时，直线PQ与⊙O相切；
当0≤t＜$\frac{2}{3}$或8＜t≤$\frac{26}{3}$（单位秒）时，直线PQ与⊙O相交；
当$\frac{2}{3}$＜t＜8时，直线PQ与⊙O相离．

点评 此题主要考查了直线与圆的位置关系，若圆的半径为r，圆心到直线的距离为d，d＞r时，圆和直线相离；d=r时，圆和直线相切；d＜r时，圆和直线相交．