
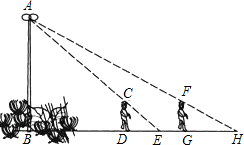
 一天晚上,小丽和小华在广场上散步,看见广场上有一路灯杆AB(如图),爱动脑筋的小丽和小华想利用投影知识来测量路灯杆AB的高度.请看下面的一段对话:
一天晚上,小丽和小华在广场上散步,看见广场上有一路灯杆AB(如图),爱动脑筋的小丽和小华想利用投影知识来测量路灯杆AB的高度.请看下面的一段对话:分析 根据AB⊥BH,CD⊥BH,FG⊥BH,可得:△ABE∽△CDE,则有$\frac{CD}{AB}=\frac{DE}{DE+BD}$和$\frac{FG}{AB}$=$\frac{HG}{HG+DG+BD}$,而$\frac{CD}{AB}$=$\frac{FG}{AB}$,即$\frac{DE}{DE+BD}$=$\frac{HG}{HG+DG+BD}$,从而求出BD的长,再代入前面任意一个等式中,即可求出AB.
解答 解:根据题意得:AB⊥BH,CD⊥BH,FG⊥BH,
在Rt△ABE和Rt△CDE中,
∵AB⊥BH,CD⊥BH,
∴CD∥AB,
可证得:
△ABE∽△CDE,
∴$\frac{CD}{AB}=\frac{DE}{DE+BD}$①,
同理:$\frac{FG}{AB}$=$\frac{HG}{HG+DG+BD}$②,
又CD=FG=1.6m,
由①、②可得:$\frac{DE}{DE+BD}$=$\frac{HG}{HG+DG+BD}$,
即$\frac{4}{4+BD}$=$\frac{6}{12+BD}$,
解得:BD=12m,
将BD=12代入①得:AB=6.4m,
答:该杆AB的高度为6.4米.
点评 本题考查了中心投影及相似三角形的应用,解这道题的关键是将实际问题转化为数学问题,本题只要把实际问题抽象到相似三角形中,利用相似比列出方程即可求出.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
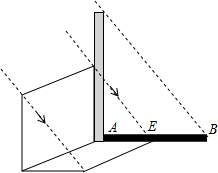 如图,一块长方形木板紧靠着一根直立于地面的木杆,其中木杆在太阳光下的投影已经画出(图中线段AB),画出此时长方形木板在地面上的投影示意图.
如图,一块长方形木板紧靠着一根直立于地面的木杆,其中木杆在太阳光下的投影已经画出(图中线段AB),画出此时长方形木板在地面上的投影示意图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com