
【题目】如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,交AC于点F,过点E作EG//BC交AC于点G.
(1)求证: AE=AF;
(2)若AG=4,AC=7,求FG的长.
【答案】
(1)解:∵BF平分∠ABC
∴∠ABF=∠CBF
∵∠AFB=180°-∠ABF-∠BAF
∠BED=180°-∠CBF-∠ADB
又∵∠BAC=∠ADB
∴∠AFB=∠BED
∵∠AEF=∠BED
∴∠AFB=∠AEF
∴AE=AF
(2)解:如图,在BC上截取BH=AB,连接FH

在△ABF和△HBF中
∵ 
∴△ABF≌△HBF(SAS)
∴AF=FH,∠AFB=∠HFB
∵∠AFB=∠AEF
∴∠HFB=∠AEF
∴AE∥FH
∴∠GAE=∠CFH
∵EG∥BC
∴∠AGE=∠C
∵AE=AF
∴AE=FH
在△AEG和△FHC中
∵ 
∴△AEG≌△FHC(AAS)
∴AG=FC=4
∴FG=AG+ FC -AC=1
【解析】(1)根据角平分线性质和三角形内角和定理,∠AFB=∠BED,再根据对顶角相等,得到∠AFB=∠AEF,根据等角对等边得到AE=AF;(2)根据全等三角形的判定方法SAS,得到△ABF≌△HBF,得到对应边、对应角相等;再由EG∥BC,根据AAS得到△AEG≌△FHC,得到对应边AG=FC,求出FG=AG+ FC -AC的值.


科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作DF⊥AC,垂足为点F.
(1)求证:DF是⊙O的切线;
(2)分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点P位于x轴上方,位于y轴的左边,且距x轴的距离为2个单位长度,距y轴的距离为3个单位长度,则点P的坐标是( )
A.(2,﹣3)
B.(2,3)
C.(3,﹣2)
D.(﹣3,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国的数学研究具有悠久的历史,《九章算术》是我国的一部古典数学名著,但对其成书的年代说法不一,一般认为在公元前后,距今约2 000年.将2 000用科学记数法表示为( )
A.2×103
B.2×104
C.20×103
D.0.2×103
查看答案和解析>>
科目:初中数学 来源: 题型:
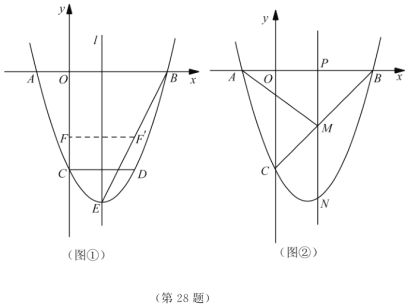
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() .点
.点![]() 在函数图像上,
在函数图像上,![]() 轴,且
轴,且![]() ,直线
,直线![]() 是抛物线的对称轴,
是抛物线的对称轴,![]() 是抛物线的顶点.
是抛物线的顶点.
(1)求![]() 、
、![]() 的值;
的值;
(2)如图①,连接![]() ,线段
,线段![]() 上的点
上的点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 恰好在线段
恰好在线段![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)如图②,动点![]() 在线段
在线段![]() 上,过点
上,过点![]() 作
作![]() 轴的垂线分别与
轴的垂线分别与![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() .试问:抛物线上是否存在点
.试问:抛物线上是否存在点![]() ,使得
,使得![]() 与
与![]() 的面积相等,且线段
的面积相等,且线段![]() 的长度最小?如果存在,求出点
的长度最小?如果存在,求出点![]() 的坐标;如果不存在,说明理由.
的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点A关于x轴的对称点为(-2,3),则点A关于y轴的对称点为( )
A. (-2,-3) B. (2,-3) C. (-2,3) D. (2,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期浙江大学的科学家们研制出今为止世界上最轻的材料,这种被称为“全碳气凝胶”的固态材料密度仅每立方厘米0.00016克,数据0.00016用科学记数法表示应是( )
A.1.6×104
B.0.16×10﹣3
C.1.6×10﹣4
D.16×10﹣5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com