
分析 (1)因为25<26<30,所以把x=26代入y=40-x即可求出该产品的年销售量为多少万件;
(2)由(1)中y于x的函数关系式和根据年获利=年销售收入-生产成本-投资成本,得到w和x的二次函数关系,再有x的取值范围不同分别讨论即可知道该公司是盈利或亏损情况;
(3)由题目的条件得到w和x在自变量x的不同取值范围的函数关系式,由w≥67.5,分别求出对应x的范围,结合y于x的关系中的x取值范围即可确定此时销售单价的范围.
解答 解:(1)∵25≤26≤30,y=$\left\{\begin{array}{l}{40-x}&{(25≤x≤30)}\\{25-0.5x}&{(30<x≤35)}\end{array}\right.$,
∴把x=26代入y=40-x得,y=14(万件),
答:当销售单价定为26元时,该产品的年销售量为14万件;
(2)①当 25≤x≤30时,W=(40-x)(x-20)-25-100
=-x2+60x-925
=-(x-30)2-25,
故当x=30时,W最大为-25,即公司最少亏损25万;
②当30<x≤35时,W=(25-0.5x)(x-20)-25-100
=-$\frac{1}{2}$x2+35x-625
=-$\frac{1}{2}$(x-35)2-12.5
故当x=35时,W最大为-12.5,即公司最少亏损12.5万;
综上,投资的第一年,公司亏损,最少亏损是12.5万;
答:投资的第一年,公司亏损,最少亏损是12.5万.
(3)①当25≤x≤30时,W=(40-x)(x-20-1)-12.5-10=-x2+61x-862.5≥67.5,
-x2+61x-862.5≥67.5,
化简得:x2-61x+930≤0
解得:30≤x≤31,
当两年的总盈利不低于67.5万元时,x=30;
②当30<x≤35时,W=(25-0.5x)(x-20-1)-12.5-10=-$\frac{1}{2}$x2+35.5x-547.5≥67.5,
化简得:x2-71x+1230≤0
解得:30≤x≤41,
当两年的总盈利不低于67.5万元时,30<x≤35,
答:到第二年年底,两年的总盈利不低于67.5万元,此时销售单价的范围是30≤x≤35.
点评 本题主要考查二次函数的实际应用能力及二次函数与一元二次不等式间关系,理解题意准确抓住相等关系是解题的关键,结合题意分类去求是解题的难点.


科目:初中数学 来源: 题型:选择题
| A. | 4,5 | B. | 4,4 | C. | 5,4 | D. | 5,5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
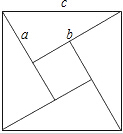 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示,如果小正方形的面积为3,直角三角形中较小的锐角为30°,那么大正方形的面积为12+6$\sqrt{3}$.
2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示,如果小正方形的面积为3,直角三角形中较小的锐角为30°,那么大正方形的面积为12+6$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①④ | B. | ③④ | C. | ②③ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平行四边形ABCD中,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于N,交BD于F,连结AF、CE.
如图,平行四边形ABCD中,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于N,交BD于F,连结AF、CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com